6 Testes de Hipóteses

6.1 Conceitos Básicos

Uma hipótese estatística é uma afirmação sobre o parâmetro $\theta$ (ou a família $\mathcal{P}$). No caso usual, tem-se duas hipóteses: $H_0: ~\theta\in\Theta_0~$, chamada de hipótese nula, e $H_1: ~\theta\in\Theta_1={\Theta}_0^c~$, chamada hipótese alternativa.

$~$

Um teste de hipótese é uma regra de decisão $\varphi: \mathfrak{X} \longrightarrow \{0,1\}$, onde $\varphi(\boldsymbol{x})=1$ significa rejeitar $H_0$ (aceitar $H_1$) e $\varphi(\boldsymbol x)=0$, não rejeitar (aceitar) $H_0$.

$~$

Se rejeita-se $H_0$ (aceita-se $H_1$) quando $H_0$ é verdadeira, comete-se um erro do tipo I. Por outro lado, se não rejeita-se $H_0$ (aceita $H_0$) quando $H_0$ é falso, ocorre um erro do tipo II.

$~$

O conjunto $\varphi^{-1}(1)=\{\boldsymbol{x} \in \mathfrak{X} :~ \varphi(\boldsymbol{x})=1\}$ recebe o nome de região de rejeição (ou região crítica). A função de poder do teste $\varphi$ é ${\pi}_\varphi(\theta)$ $=P\left(\varphi^{-1}(1)|\theta\right)$ $=P\big(\text{'Rejeitar $H_0$'} | \theta\big)$.

$~$

Dizemos que um teste $\varphi$ tem nível de significância $\alpha$ se $\displaystyle\sup_{\theta\in\Theta_0}\pi_\varphi(\theta)\leq \alpha$. Se $\alpha=\displaystyle\sup_{\theta\in\Theta_0}\pi_\varphi(\theta)$ dizemos que o teste é de tamanho $\alpha$.

$~$

Uma hipótese é dita simples se contém apenas um ponto, $H:\theta=\theta_0$. Caso contrário é chamada de hipótese composta. No caso em que $H:\theta\in\Theta_0$ é tal que $\dim(\Theta_0)<\dim(\Theta)$, diz-se que $H$ é uma hipótese precisa (“sharp”).

$~$

6.2 Revisão: Abordagem Frequentista

Um teste de hipótese “ideal” seria aquele que as probabilidades de erros tipo I e tipo II são iguais a zero, isto é, $\pi_\varphi(\theta)=0$, $\forall \theta \in \Theta_0$, e $\pi_\varphi(\theta)=1$, $\forall \theta \in \Theta_1$. Contudo, não é possível obter tais testes em geral.

A solução usual é fixar um nível de significância $\alpha$ e considerar apenas a classe de teste de nível $\alpha$, isto é, testes tais que $\displaystyle\sup_{\theta\in\Theta_0}\pi_\varphi(\theta) \leq \alpha$. Os testes ótimos sob o ponto de vista frequentista são aqueles na classe de testes de nível $\alpha$ que tenha maior função poder ${\pi}_\varphi(\theta)$ para $\theta \in \Theta_1$. Um teste que satisfaz isso é chamado de Teste Uniformemente Mais Poderoso (UMP) mas testes com essa propriedade também só podem ser obtidos em casos específicos.

$~$

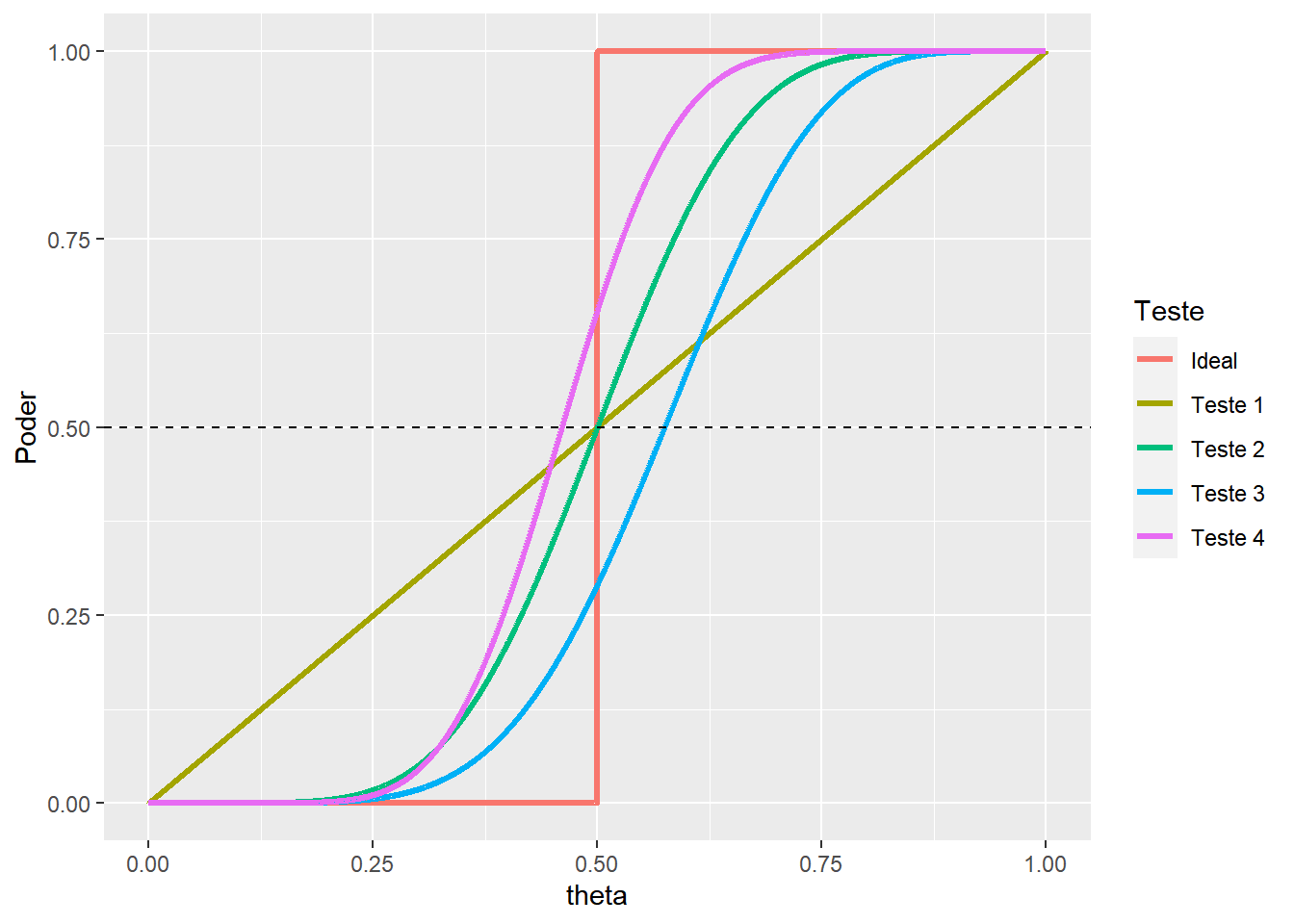
Exemplo. Considere que $\Theta=[0,1]$ e deseja-se testar $H_0: \theta \leq 0.5$ contra $H_1: \theta > 0.5$. O gráfico a seguir ilustra as funções poder de quatro testes disponíveis para esse problema. Supondo (apenas para fins didáticos) que $\alpha=0.5$, temos que o teste UMP de nível $\alpha$ é o teste 2. O teste 4, apesar de ser mais poderoso, não é um teste de nível $\alpha$.

$~$

Uma das situações onde é possível obter o teste mais poderoso é o caso que as hipóteses nula e alternativa são simples, isto é, $H_0:\theta=\theta_0$ contra $H_1:\theta=\theta_1$. Nesses casos, pode-se considerar o Lema de Neyman-Pearson, que afirma que o teste mais poderoso é dado por

${\varphi}^*(\boldsymbol x)=\left\{\begin{array}{rl} 1,& \dfrac{f(x|\theta_0)}{f(x|\theta_1)}\leq k\\ 0,& c.c.\end{array}\right.~.$

Além disso, o teste ${\varphi}^*$ minimiza a combinação linear das probabilidades de erro $a\alpha+b\beta$ com $k=b/a$, $\alpha={\pi}_{{\varphi}^*}(\theta_0)$ $=P(\textrm{'erro tipo I'})$ e $\beta=1-{\pi}_{{\varphi}^*}(\theta_1)$ $=P(\textrm{'erro tipo II'})$.

$~$

Como dito anteriorimente, usualmente é fixado um nível $\alpha$ e isso permite encontrar o valor de $k$ de modo que o teste construído a partir do lema é o teste mais poderoso de nível $\alpha$. Assim,

$\alpha$ $={\pi}_{\varphi^*}(\theta_0)$ $=P\left(\boldsymbol X \in {\varphi}^{-1}(\{1\})|\theta_0\right)$ $=P\left(\left\{\boldsymbol x: \dfrac{f(\boldsymbol x|\theta_0)}{f(\boldsymbol x|\theta_1)} \leq k\right\}\Big|\theta_0\right)$.

Suponha que foi observado $\boldsymbol X = \boldsymbol x_o$, é possível calcular o nível descritivo (ou p-value) da seguinte forma:

$p(\boldsymbol x_o)$ $=P\left(\left\{\boldsymbol x: \dfrac{f(\boldsymbol x|\theta_0)}{f(\boldsymbol x|\theta_1)} \leq \dfrac{f(\boldsymbol x_o|\theta_0)}{f(\boldsymbol x_o|\theta_1)}\right\}\Big|\theta_0\right)$

$~$

É possível obter testes UMP em alguns casos particulares. Em especial, nos casos em que a família de distribuições para $\boldsymbol X$ condicional a $\theta$ possui a propriedade de razão de verossimilhanças monótona, é possível construir testes UMP para hipóteses do tipo $H_1: \theta \leq \theta_0$ contra $H_1: \theta > \theta_0$. Para problemas onde as hipóteses são da forma $H_1: \theta = \theta_0$ contra $H_1: \theta \neq \theta_0$, bastante comuns no dia a dia de um estatístico, não existe teste UMP, em geral.

$~$

Nos casos em que não existe um teste UMP, o teste mais utilizado sob a abordagem frequentista certamente é o teste da razão de verossimilhança generalizada (RVG). Primeiramente, considere a razão de verossimilhanças generalizada, dada por

$\lambda(\boldsymbol x)=\dfrac{\displaystyle \sup_{\theta\in\Theta_0} f(\boldsymbol x|\theta)}{\displaystyle \sup_{\theta\in\Theta} f(\boldsymbol x|\theta)}$.

Note que $0\leq \lambda(\boldsymbol x) \leq 1$, $\forall ~\boldsymbol x \in \mathfrak{X}$ e $\forall ~\Theta_0 \subseteq \Theta$. Um teste RVG é qualquer teste da forma

${\varphi}_{RV}(\boldsymbol x)=\left\{\begin{array}{rl} 1,& \lambda(\boldsymbol x) \leq k\\ 0,& c.c.\end{array}\right.~.$

$~$

Novamente, $k$ pode ser escolhido de modo que o teste resultante seja de nível $\alpha$, isto é, $\displaystyle \sup_{\theta \in \Theta_0} P\left(\lambda(\boldsymbol x) \leq k \Big | \theta\right) \leq \alpha$. Do mesmo modo, se foi observado $\boldsymbol X=\boldsymbol x_o$, um p-value é $p(\boldsymbol x_o)$ $=\displaystyle \sup_{\theta \in \Theta_0}P\left(\left\{\boldsymbol x: \lambda(\boldsymbol x) \leq \lambda(\boldsymbol x_o)\right\}\big|\theta\right)$. Por fim, em casos onde é difícil fazer os cálculos de forma exata e o tamanho amostral $n$ é razoavelmente grande, é possível usar a distribuição assintótica da RVG $~-2\log \lambda(\boldsymbol x)\overset{\mathcal{D}}{~\longrightarrow~}\chi_d^2$, onde $d=\dim(\Theta)-\dim(\Theta_0)$.

$~$

6.3 Abordagem Bayesiana (via Teoria da Decisão)

Sob a abordagem de teoria da decisão, podemos ver um teste de hipóteses como um problema de decisão onde temos duas possíveis decisões $\mathcal{D}=\{d_0,d_1\}$, onde $d_0$ é decidir por $H_0:\theta \in \Theta_0$ e $d_1$ é decidir por $H_1:\theta \in \Theta_1$, com $\Theta=\Theta_0\cup\Theta_1$. Um teste de hipóteses nesse contexto é uma função de decisão $\varphi: \mathfrak{X} \longrightarrow \{0,1\}$, de modo que quando $\varphi(\boldsymbol x)=i$, decide-se por $d_i$, $i\in \{0,1\}$.

$~$

Primeiramente, considere o contexto apresentado no Lema de Neyman-Pearson, onde $\Theta=\{\theta_0,\theta_1\}$ e deseja-se testar $H_0: \theta=\theta_0$ contra $H_1: \theta = \theta_1$. Considere que, a priori, $f(\theta_0) = \pi$, a função de verossimilhança é $f(\boldsymbol x |\theta)$ e a função de perda apresentada na tabela a seguir.

$L(d,\theta)$	$\theta_0$	$\theta_1$
$d_0$	$0$	$b$
$d_1$	$a$	$0$

Então, o risco de uma função de decisão $\varphi$ é

$\rho(\varphi,P)$ $=E\left[L(\varphi(\boldsymbol X),\theta)\right]$ $= \pi~E\left[L(\varphi(\boldsymbol X),\theta)\big|\theta_0)\right] + (1-\pi)E\left[L(\varphi(\boldsymbol X),\theta)\big|\theta_1)\right]$ $= a~\pi~P\left(\varphi(\boldsymbol x)=1\big|\theta_0\right) + b~(1-\pi)~P\left(\varphi(\boldsymbol x)=0\big|\theta_1\right)$ $= a~\pi~\alpha_\varphi + b~(1-\pi)~\beta_\varphi$

Como o risco acima é uma combinação linear das probabilidades dos erro tipo I e tipo II, podemos aplicar o Lema de Neyman-Pearson e obter a função de decisão $\varphi^*$ que minimiza o risco

${\varphi}^*(\boldsymbol x)=\left\{\begin{array}{rl} 1,& \dfrac{f(x|\theta_0)}{f(x|\theta_1)}\leq \dfrac{b~(1-\pi)}{a~\pi}\\ 0,& c.c.\end{array}\right.~.$

Esse resultado é apresentado por DeGroot (1986) e é uma espécie de Lema de Neyman-Pearson Generalizado.

$~$

A solução para esse mesmo problema pode também ser obtida usando a forma extensiva. O risco posterior para as suas decisões é $r_x(d_0) = b f(\theta_1|\boldsymbol x)$ e $r_x(d_1) = a f(\theta_0|\boldsymbol x)$, de modo que rejeitamos $H_0$ (decidimos por $d_1$ ou $\varphi(\boldsymbol x)=1$) se

$r_x(d_1) \leq r_x(d_0)$ $\Longleftrightarrow a f(\theta_0|\boldsymbol x) \leq b f(\theta_1|\boldsymbol x)$ $\Longleftrightarrow a f(\theta_0|\boldsymbol x) \leq b \left[1-f(\theta_0|\boldsymbol x)\right]$ $\Longleftrightarrow f(\theta_0|\boldsymbol x) \leq \dfrac{b}{a+b}$

De modo que o teste de Bayes também pode ser apresentado como

${\varphi}^*(\boldsymbol x)=\left\{\begin{array}{rl} 1,& f(\theta_0|\boldsymbol x) \leq \dfrac{b}{a+b} \\ 0,& c.c.\end{array}\right.~.$

A interpreção nesse caso é mais direta, a hipótese é rejeitada se sua probabilidade posterior é “pequena.” Como vimos, essas soluções são equivalentes. De fato,

$f(\theta_0|\boldsymbol x)$ $=\dfrac{f(\theta_0)f(\boldsymbol x|\theta_0)}{f(\boldsymbol x)}$ $=\pi~\dfrac{f(\boldsymbol x|\theta_0)}{f(\boldsymbol x)}$;
$f(\theta_1|\boldsymbol x)$ $=\dfrac{f(\theta_1)f(\boldsymbol x|\theta_1)}{f(\boldsymbol x)}$ $=(1-\pi)~\dfrac{f(\boldsymbol x|\theta_1)}{f(\boldsymbol x)}$.

Assim,

$r_x(d_1) \leq r_x(d_0)$ $\Longleftrightarrow a \pi~\dfrac{f(\boldsymbol x|\theta_0)}{f(\boldsymbol x)} \leq b (1-\pi)~\dfrac{f(\boldsymbol x|\theta_1)}{f(\boldsymbol x)}$ $\Longleftrightarrow \dfrac{f(\boldsymbol x|\theta_0)}{f(\boldsymbol x|\theta_1)} \leq \dfrac{b (1-\pi)}{a \pi}$.

$~$

Considere agora um caso mais geral, onde $\Theta=\Theta_0 \dot{\cup} \Theta_1$ e deseja-se testar $H_0: \theta \in \Theta_0$ contra $H_1: \theta \in \Theta_1$. Considere também a função de perda mais geral apresentada a seguir, com $a_0 \leq a_1$ e $b_0 \leq b_1$.

$L(d,\theta)$	$\Theta_0$	$\Theta_1$
$d_0$	$a_0$	$b_1$
$d_1$	$a_1$	$b_0$

O risco posterior de cada uma das decisões é

$r_x(d_1,\theta)$ $=a_1P(\theta\in\Theta_0|x)+b_0-b_0P(\Theta_0|x)$,

De modo que rejeita-se $H_0$, $\varphi(\boldsymbol x)=1$, se

$r_x(d_1,P)\leq r_x(d_0,P)$ $\Leftrightarrow (a_1-b_0)P(\Theta_0|x)+b_0 \leq (a_0-b_1)P(\Theta_0|x)+b_1$ $\Leftrightarrow P(\Theta_0|x) \leq \dfrac{(b_1-b_0)}{(a_1-a_0)+(b_1-b_0)}$

Assim, o teste de bayes nesse caso é

${\varphi}(\boldsymbol x)=\left\{\begin{array}{rl} 1,& P(\Theta_0|x) \leq \dfrac{(b_1-b_0)}{(a_1-a_0)+(b_1-b_0)} \\ 0,& c.c.\end{array}\right.~.$

$~$

6.4 Probabilidade Posterior de $H_0$

Resultado. Seja $\Theta=\Theta_0 \dot{\cup} \Theta_1$ e suponha que deseja-se testar $H_0: \theta \in \Theta_0$ contra $H_1: \theta \in \Theta_1$ considerando a função de perda a seguir, com $a_0 \leq a_1$ e $b_0 \leq b_1$.

$L(d,\theta)$	$\Theta_0$	$\Theta_1$
$d_0$	$a_0$	$b_1$
$d_1$	$a_1$	$b_0$

Então, o teste de bayes é

${\varphi}(\boldsymbol x)=\left\{\begin{array}{rl} 1,& P(\Theta_0|x) \leq \dfrac{(b_1-b_0)}{(a_1-a_0)+(b_1-b_0)} \\ 0,& c.c.\end{array}\right.$.

$~$

Exemplo 1. Considere $X_1,\ldots,X_n$ c.i.i.d. tais que $X_i|\theta \sim Ber(\theta)$ com $\Theta = \left\{1/2,3/4\right\}$. Suponha que, a priori, $f(\theta=1/2)=f(\theta=3/4)=1/2$ e deseja-se testar $H_0: \theta=1/2$ contra $H_1: \theta=3/4$. Tem-se que $T(\boldsymbol X)=\sum X_i~|~\theta\sim Bin(n,\theta)$ é uma estatística suficiente para $\theta$. Então,

$P(\theta=1/2|T(\boldsymbol X)=t)$ $=\dfrac{f(t|\theta=1/2)f(\theta=1/2)}{\displaystyle\sum_{\theta \in \left\{1/2~,~3/4\right\}} f(t|\theta)f(\theta)}$ $=\dfrac{\displaystyle\binom{n}{t}\left(\dfrac{1}{2}\right)^n}{\displaystyle\binom{n}{t}\left(\dfrac{1}{2}\right)^n+\binom{n}{t}\left(\dfrac{3}{4}\right)^t\left(\dfrac{1}{4}\right)^{n-t}}$ $=\dfrac{1}{1+\dfrac{3^t}{2^n}}$.

$~$

Considere a função de perda $L(d,\theta) = a_0~\mathbb{I}(d_0,\Theta_0) + b_1~\mathbb{I}(d_0,\Theta_1) + a_1~\mathbb{I}(d_1,\Theta_0) + b_0~\mathbb{I}(d_1,\Theta_1)$ como no resultado anterior. Então, rejeita-se $H_0$ se $P(\theta \in \Theta_0 | \boldsymbol x) < K$, com $K = \dfrac{b_1-b_0}{(a_1-a_0)+(b_1-b_0)}$. Assim,

$P(\theta=1/2|T=t)\leq K$ $~\Longleftrightarrow~ \dfrac{1}{1+\frac{3^t}{2^n}} \leq K$ $~\Longleftrightarrow~ {1+\dfrac{3^t}{2^n}} \geq \dfrac{1}{K}$ $~\Longleftrightarrow~ 3^t\geq 2^n\left(\dfrac{1}{K}-1\right)$ $~\Longleftrightarrow~ t\geq n\log_3(2)+\log_3\left(\dfrac{1-K}{K}\right)$ $~\Longleftrightarrow~ t\geq nlog_3(2)+log_3\left(\dfrac{a_1-a_0}{b_1-b_0}\right)$.

$~$

Tomando $a_1=b_1=1$ e $a_0=b_0=0$, rejeita $H$ se

$\sum X_i \geq n\log_3(2)+\log_3(1)$ $~\Longleftrightarrow~ \sum X_i \geq n\log_3(2)$ $~\Longrightarrow~ \bar{X} \geq \log_3(2)\approx 0,631$.

$~$

O teste de Bayes é

${\varphi}(\boldsymbol x) =\left\{\begin{array}{rl} 1,& f(\theta=1/2|\boldsymbol x) \leq \dfrac{(b_1-b_0)}{(a_1-a_0)+(b_1-b_0)} = \dfrac{1}{2} \\ 0,& c.c.\end{array}\right.$ $~\Longrightarrow~ {\varphi}(\boldsymbol x) =\left\{\begin{array}{rl} 1,& \bar{X} \geq \log_3(2) \\ 0,& c.c.\end{array}\right.$.

$~$

Exemplo 2: $X_1,...,X_n$ c.i.i.d. tais que $X_i|\theta\sim N(\theta,{\sigma}_0^2)$ com ${\sigma}_0^2$ conhecido. Suponha que, a priori, $\theta \sim N(m,v^2)$ e $\bar{X}$ é estatística suficiente para $\theta$ com $\bar{X}|\theta \sim \left(\theta,{\sigma}_0^2/n\right)$, de modo que $\theta|\boldsymbol X \sim N\left(\dfrac{{\sigma}_0^2~m+nv^2~\bar x}{{\sigma}_0^2+nv^2}~,~\dfrac{{\sigma}_0^2~v^2}{{\sigma}_0^2+nv^2}\right)$. Suponha ainda que o objetivo é testar $H_0: \theta\leq \theta_0$ contra $H_1:\theta > \theta_0$.

$~$

Utilizando novamente o resultado anterior, temos

$P\left(\theta\in\Theta_0|\boldsymbol x\right)$ $= P\left(\theta \leq \theta_0|\boldsymbol x\right)$ $= P\left(Z\leq\dfrac{\theta_0-\frac{{\sigma}_0^2~m+nv^2~\bar x}{{\sigma}_0^2+nv^2}}{\sqrt{\frac{{\sigma}_0^2~v^2}{{\sigma}_0^2+nv^2}}}~\Bigg|~\bar x\right)$ $= \Phi\left(\dfrac{\theta_0-\frac{{\sigma}_0^2~m+nv^2~\bar x}{{\sigma}_0^2+nv^2}}{\sqrt{\frac{{\sigma}_0^2~v^2}{{\sigma}_ 0^2+nv^2}}}\right)$ $= \Phi\left(\dfrac{({\sigma}_0^2+nv^2)\theta_0-{\sigma}_0^2~m-nv^2~\bar x}{{\sigma}_0~v~\sqrt{{\sigma}_ 0^2+nv^2}}\right)$,

e deve-se rejeitar $H_0$ se

$P\left(\theta\in\Theta_0|\boldsymbol x\right) \leq \dfrac{(b_1-b_0)}{(a_1-a_0)+(b_1-b_0)} = K$ $~\Longleftrightarrow~\Phi\left(\dfrac{({\sigma}_0^2+nv^2)\theta_0-{\sigma}_0^2~m-nv^2~\bar x}{{\sigma}_0~v~\sqrt{{\sigma}_ 0^2+nv^2}}\right) \leq K$ $~\Longleftrightarrow~ \bar x ~\geq~ \dfrac{({\sigma}_0^2+nv^2)\theta_0-{\sigma}_0^2~m}{nv^2} - {\Phi}^{-1}(K)\dfrac{{\sigma}_0~\sqrt{{\sigma}_ 0^2+nv^2}}{nv}$ $~\Longleftrightarrow~ \bar x ~\geq~ \dfrac{{\sigma}_0^2(\theta_0-m)+nv^2\theta_0}{nv^2} - {\Phi}^{-1}(K)\dfrac{{\sigma}_0~\sqrt{{\sigma}_ 0^2+nv^2}}{nv}$.

$~$

Se $a_0=b_0=0$ e $a_1=b_1=1$, então $\Phi^{-1}(K=1/2)=0$ e rejeita-se $H_0$ se

$\bar x ~\geq~ \dfrac{{\sigma}_0^2(\theta_0-m)+nv^2\theta_0}{nv^2} ~\underset{n\uparrow\infty}{\longrightarrow}~ \theta_0$.

$~$

6.5 Fator de Bayes

Voltando ao resultado, tem-se que rejeita-se $H_0$ se

$r_x(d_0) \geq r_x(d_1)$ $~\Longleftrightarrow~ a_0P(\Theta_0|\boldsymbol x)+b_1P(\Theta_1|\boldsymbol x) \geq a_1P(\Theta_0|\boldsymbol x)+b_0P(\Theta_1|\boldsymbol x)$ $~\Longleftrightarrow~ \dfrac{P(\Theta_0|\boldsymbol x)}{P(\Theta_1|\boldsymbol x)}\leq\dfrac{b_1-b_0}{a_1-a_0}$

$~\Longleftrightarrow~ BF(\boldsymbol x)$ $=\dfrac{\frac{P(\Theta_0|\boldsymbol x)}{P(\Theta_1|\boldsymbol x)}}{\frac{P(\Theta_0)}{P(\Theta_1)}}$ $=\dfrac{\frac{P(\Theta_0|\boldsymbol x)}{P(\Theta_0)}}{\frac{P(\Theta_1|\boldsymbol x)}{P(\Theta_1)}}$ $=\dfrac{f(\boldsymbol x | \Theta_0)}{f(\boldsymbol x | \Theta_1)}$ $\leq \dfrac{(b_1-b_0)}{(a_1-a_0)}\dfrac{P(\Theta_1)}{P(\Theta_0)}$,

onde $BF$ é o Fator de Bayes, frequentemente utilizado na literatura bayesiana para testar hipóteses. Ele pode ser visto como uma razão de chances que representa o aumento na chance da hipótese nula ser mais plausível que a hipótese alternativa após observar os dados em relação a sua opinião a priori. O $BF$ também pode ser reescrito como

$BF(\boldsymbol x)$ $=\dfrac{f_0(\boldsymbol x)}{f_1(\boldsymbol x)}$ $=\dfrac{f(\boldsymbol x | \Theta_0)}{f(\boldsymbol x | \Theta_1)}$ $=\dfrac{\displaystyle \int_{\Theta}f(\boldsymbol x|\theta) f(\theta|\Theta_0) d\theta} {\displaystyle \int_{\Theta} f(\boldsymbol x|\theta)f(\theta|\Theta_1)d\theta}$ $=\dfrac{\displaystyle \int_{\Theta_0}f(x|\theta)dP_0(\theta)}{\displaystyle \int_{\Theta_1}f(x|\theta)dP_1(\theta)}$ $=\dfrac{E\left[f(\boldsymbol x|\theta)|\theta\in\Theta_0\right]}{E\left[f(\boldsymbol x|\theta)|\theta \in \Theta_1\right]}$.

$~$

No exemplo 1. Lembrando que, a priori, $P(\theta=1/2)=P(\theta=3/4)=1/2$ e considerando novamente $a_0=b_0=0$ e $a_1=b_1=1$, temos que devemos rejeitar $H_0$ se $BF(\boldsymbol x)<\frac{(b_1-b_0)}{(a_1-a_0)}\frac{P(\theta=1/2)}{P(\theta=3/4)}=1$. Então,

$BF(\boldsymbol x)=\dfrac{P(\theta=1/2|\boldsymbol x)}{P(\theta=3/4|\boldsymbol x)}\dfrac{1/2}{1/2}$ $=\dfrac{\frac{1}{1+3^t/2^n}}{\frac{3^t/2^n}{1+3^t/2^n}}$ $=\dfrac{2^n}{3^t}\leq 1$ $~\Longleftrightarrow~ \bar{x} \geq \log_3(2)$,

de modo que a decisão baseada no fator de Bayes concorda com o resultado baseado na probabilidade a posteriori da hipótese.

$~$

No exemplo 2. $\theta|\boldsymbol X \sim N\left(\dfrac{{\sigma}_0^2~m+nv^2~\bar x}{{\sigma}_0^2+nv^2}~,~\dfrac{{\sigma}_0^2~v^2}{{\sigma}_0^2+nv^2}\right)$ e o objetivo é testar $H_0: \theta\leq \theta_0$ contra $H_1:\theta > \theta_0$. A probabilidade a posteriori da hipótese $H_0$ é

$P\left(\theta\in\Theta_0|\boldsymbol x\right)$ $= \Phi\left(\dfrac{({\sigma}_0^2+nv^2)\theta_0-{\sigma}_0^2~m-nv^2~\bar x}{{\sigma}_0~v~\sqrt{{\sigma}_ 0^2+nv^2}}\right)$,

e, a priori, $P(\theta \in \Theta_0)$ $=P(\theta \leq \theta_0)$ $= \Phi\left(\dfrac{\theta_0-m}{v}\right)$, de modo que o fator de Bayes nesse caso é

$BF(\boldsymbol x)$ $= \dfrac{P(\Theta_0|\boldsymbol x)}{P(\Theta_1|\boldsymbol x)} \dfrac{P(\Theta_1)}{P(\Theta_0)}$ $= \dfrac{\Phi\left(\frac{({\sigma}_0^2+nv^2)\theta_0-{\sigma}_0^2~m-nv^2~\bar x}{{\sigma}_0~v~\sqrt{{\sigma}_0^2+nv^2}}\right)}{\left[1-\Phi\left(\frac{({\sigma}_0^2+nv^2)\theta_0-{\sigma}_0^2~m-nv^2~\bar x}{{\sigma}_0~v~\sqrt{{\sigma}_0^2+nv^2}}\right)\right]} ~ \dfrac{\left[1-\Phi\left(\frac{\theta_0-m}{v}\right)\right]}{\Phi\left(\frac{\theta_0-m}{v}\right)}$.

$~$

m=0; v2=1 # Média e Variância da Priori
sigma02=1 # Variância Populacional (conhecido)
n=3 # tamanho amostral
theta0=1 # H0: theta <= theta0
a0=0; b0=0; a1=1; b1=1 # Função de Perda
K1=(b1-b0)/(a1-a0+b1-b0) # corte Prob. Posterior
K2=((b1-b0)*(1-pnorm((theta0-m)/sqrt(v2)))) / ((a1-a0)*pnorm((theta0-m)/sqrt(v2))) #corte Fator de Bayes
K3=((sigma02+n*v2)*theta0-sigma02*m)/(n*v2) - qnorm(K1)*sqrt(sigma02*(sigma02+n*v2))/(n*sqrt(v2)) # corte xbar
# Probabilidade a Posteriori de H0 (como função de Xbar)
postH = function(xbar){
  pnorm(((sigma02 + n*v2)*theta0 - sigma02*m - n*v2*xbar)/ sqrt(sigma02*v2*(sigma02+n*v2))) }
# Fator de Bayes de H0 (como função de Xbar)
bf = function(xbar){
  (postH(xbar)*(1-pnorm((theta0-m)/sqrt(v2))))/ ((1-postH(xbar))*pnorm((theta0-m)/sqrt(v2))) }
xbar=seq(0.5,2.5,0.001)
PP=postH(xbar)
BF=bf(xbar)
FS=(max(PP)-min(PP))/(max(BF)-min(BF)) # var. aux. para transformção dos eixos
tibble(xbar,PP,BF) %>%
  ggplot() +
    geom_line(aes(x=xbar,y=PP,colour="Prob. Posterior")) +
    geom_line(aes(x=xbar,y=((BF-min(BF))*FS+min(PP)),colour="Fator de Bayes"))+
    scale_y_continuous(sec.axis = sec_axis(~./FS-min(PP)/FS+min(BF), name = "BF"))+
    geom_hline(aes(yintercept=K1),lty=2, col="darkgrey") +
    geom_point(aes(x=K3,y=K1,colour="Prob. Posterior")) +
    geom_hline(aes(yintercept=((K2-min(BF))*FS+min(PP))),lty=2, col="darkgrey") +
    geom_point(aes(x=K3,y=((K2-min(BF))*FS+min(PP)),colour="Fator de Bayes")) +
    geom_vline(aes(xintercept=K3),lty=2, col="darkgrey") +
    theme_bw() + labs(colour = "")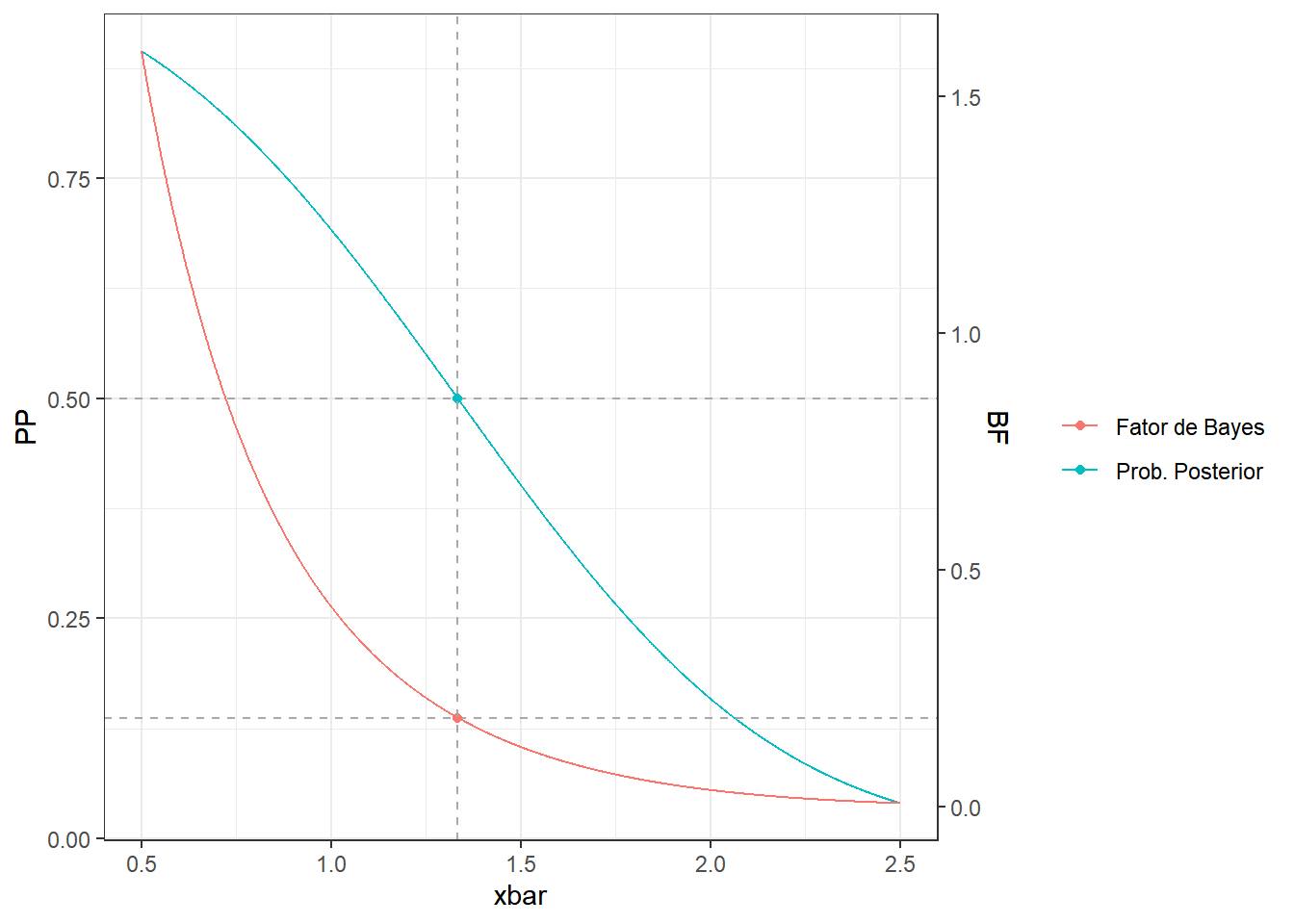

Nesse exemplo, é possível ver que tanto o Fator de Bayes quanto a probabilidade posterior da hipótese nula “ordenam” o espaço amostral, representado aqui pela estatística suficiente, $\bar{X}$. Deste modo, quanto menores os valores dessas estatísticas de teste, mais desfavorável é o ponto amostral para a hipótese nula. Como visto anteriormente, as regras de decisão baseadas nessas estatísticas são equivalentes e, portanto, a ordenação do espaço amostral é a mesma.

$~$

Problema: Suponha agora que, nesse mesmo exemplo, deseja-se testar $H_0:\theta=0$ contra $H_1: \theta\neq 0$. Como a posteriori é Normal, temos que $P(\theta \in \Theta_0|\boldsymbol x)$ $=P(\theta=0|\boldsymbol x)=0$ , $\forall~ \boldsymbol x\in \mathfrak{X}~$ e, desta forma, a hipótese nula $H_0$ sempre é rejeitada.

De fato, para qualquer cenário em que a hipótese $H_0$ tem medida nula a priori, $P(\theta \in \Theta_0)=0$, tem-se que, a posteriori, $P(\theta \in \Theta_0|\boldsymbol x)=0$. Isso ocorre frequentemente nos casos em que $H_0$ é uma hipótese precisa, isto é, $dim(\Theta_0)<dim(\Theta)$. Neste cenário, é necessário definir procedimentos alternativos para testar hipóteses.

$~$

6.6 Teste de Jeffreys

O teste de Jeffreys (1961?) consiste em atribuir uma probabilidade positiva para o conjunto que define a hipótese nula, $p_0=P(\theta \in \Theta_0)>0$.

$~$

Exemplo 2. Suponha que deseja-se testar $H_0: \theta=0$ contra $H_1: \theta\neq 0$. Suponha que sua opinião a priori é $\theta \sim Normal(0,2)$. Contudo, já foi visto que $P(\theta=0|\boldsymbol x)=0$, $\forall \boldsymbol x \in \mathfrak{X}$. Deste modo, você opta por atribuir uma probabilidade positiva $p_0=0.2$ para o ponto $\theta=0$, ou seja, você vai considerar uma distribuição mista $f(\theta)=p_0\mathbb{I}(\theta=0)+(1-p_0)f_N(\theta)$, onde $f_N$ é a densidade da $Normal(0,2)$. Sua função de distribuição a prioi, $F(\theta)=p_0~\mathbb{I}(\theta\geq0)+(1-p_0)~\Phi\left(\theta/\sqrt{2}\right)$, está representada no gráfico a seguir.

theta=c(seq(-5,-0.001,0.001),seq(0.001,5,0.001))
p=0.2
pprior = function(t){
  p*I(t>=0)+(1-p)*pnorm(t,0,2)*I(t!=0)
}
tibble(theta,Prior=pprior(theta)) %>%
  ggplot()+geom_line(aes(x=theta,y=Prior))+
    geom_point(aes(x=0,y=(1-p)*pnorm(0,0,2)))+
    geom_point(aes(x=0,y=(1-p)*pnorm(0,0,2)+p))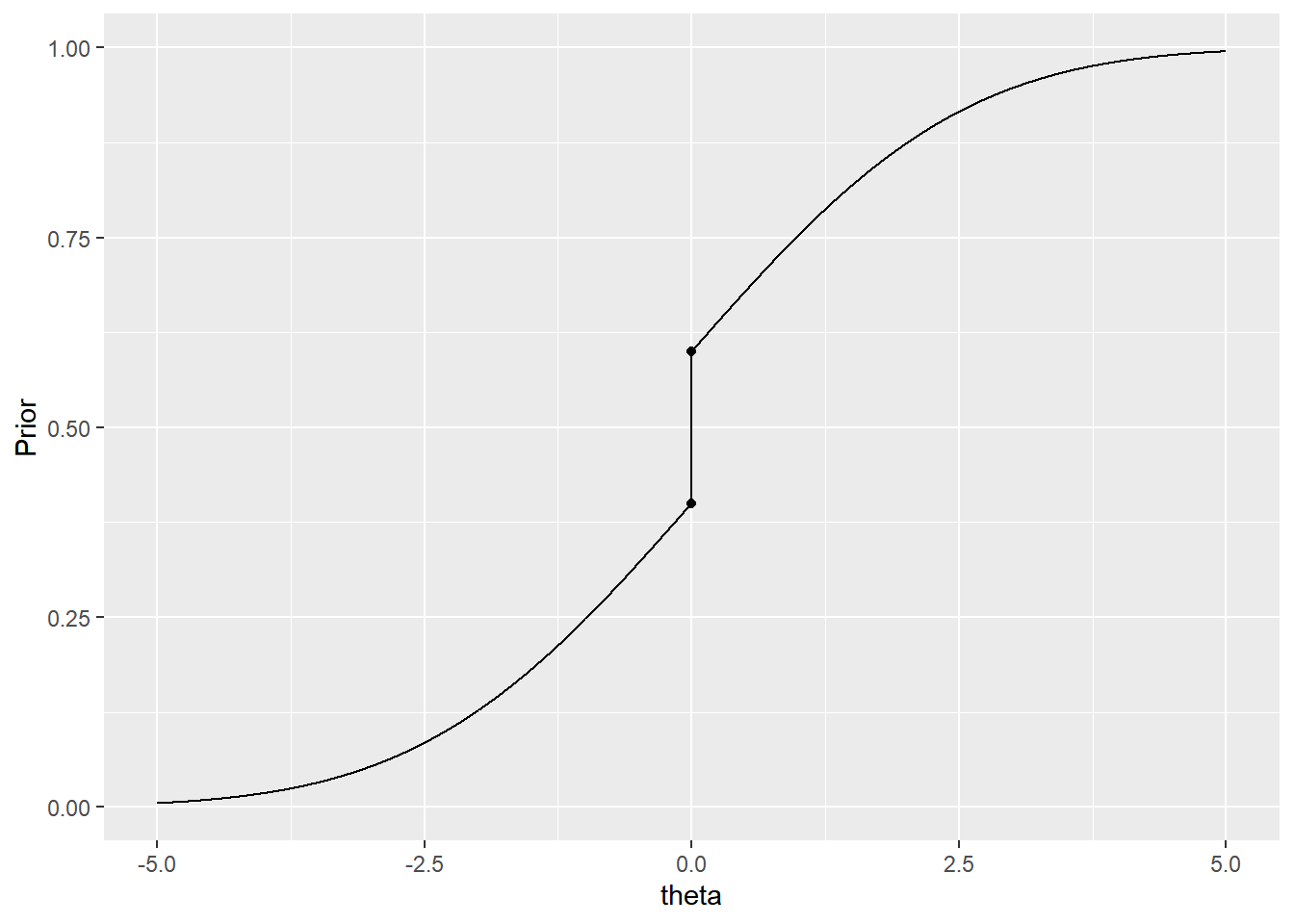

Exercício. Calcule $P(\theta=0|\boldsymbol X=\boldsymbol x)$.

$~$

Exemplo 3. Seja $X_1,\ldots,X_n$ c.i.i.d. tais que $X_i|\theta \sim Ber (\theta)$ e considere que, a priori, $\theta\sim Beta(a,b)$. Como $X=\sum X_i$ é estatística suficiente com $X\big|\theta \sim Bin(n,\theta)$, tem-se que $\theta\big|x=\sum x_i\sim Beta\left(a+\sum x_i,b+n-\sum x_i\right)$.

A distribuição marginal de $X$ é chamada distribuição preditiva a priori e pode ser calculada por

$f(x)$ $=\displaystyle \int_0^1 f(x,\theta)d\theta$ $=\displaystyle \int_0^1 f(x|\theta)f(\theta)d\theta$ $=\displaystyle \binom{n}{x}~\dfrac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}~\int_0^1 \theta^{a+x-1}(1-\theta)^{b+n-x-1}d\theta$ $=\displaystyle \binom{n}{x}~\dfrac{\Gamma(a+b)}{\Gamma(a)\Gamma(b)}~\dfrac{\Gamma(a+x)\Gamma(b+n-x)}{\Gamma(a+b+n)}$ $=\displaystyle \binom{n}{x} \dfrac{\beta(a+x,b+n-x)}{\beta(a,b)}~\mathbb{I}_{\{0,\ldots,n\}}(x)$

$\Longrightarrow X \sim Beta-Binomial(n,a,b)$.

$~$

Suponha agora que deseja-se testar $H_0: \theta=\theta_0$ contra $H_1:\theta\neq \theta_0$, com $\theta_0=1/2$, utilizando o teste de Jeffreys. Desta forma, considere $p_0=P(\theta=1/2)=1/2$ e sua priori de Jeffreys é $f_J(\theta)=p_0~\mathbb{I}(\theta=\theta_0) +(1-p_0)f_\beta(\theta)~\mathbb{I}(\theta\neq\theta_0)$, onde $f_\beta$ é a densidade da $Beta(a,b)$.

A distribuição preditiva com relação a priori $f_J$ é

$f_J(x)$ $=\displaystyle p_0f(x|\theta_0)~\mathbb{I}(\theta=\theta_0)+ (1-p_0)\overbrace{\int_0^1f(x|\theta)f_\beta(\theta)~\mathbb{I}(\theta\neq\theta_0)d\theta}^{f(x)}$ $=\displaystyle p_0\binom{n}{x}{\theta}_0^x(1-\theta_0)^{n-x}~\mathbb{I}(\theta=\theta_0) + (1-p_0)\binom{n}{x}\dfrac{\beta(a+x,b+n-x)}{\beta(a,b)}~\mathbb{I}(\theta\neq\theta_0)$,

de modo que a distribuição a posteriori é

$f_J(\theta| x)$ $= \dfrac{f( x|\theta)f_J(\theta)}{f_J(x)}$ $= \dfrac{p_0\binom{n}{x} (1/2)^n}{f_J(x)}~\mathbb{I}(\theta=1/2) +\dfrac{(1-p_0)\binom{n}{x}\theta^{a+x-1}(1-\theta)^{b+n-x-1}}{\beta(a,b)~f_J(x)}~\mathbb I(\theta\neq 1/2)$.

$~$

A probabilidade posterior da hipótese $H_0:\theta=1/2$ é

$p_x=P(\theta=1/2|x)$ $=\dfrac{p_0\binom{n}{x}(1/2)^n}{p_0\binom{n}{x}(1/2)^n+(1-p_0)\binom{n}{x}\frac{\beta(a+x,b+n-x)}{\beta(a,b)}}$ $=\dfrac{1}{1+\dfrac{(1-p_0)}{p_0}\dfrac{\beta(a+x,b+n-x)}{(1/2)^n\beta(a,b)}}$.

E, assim, o Fator de Bayes é dado por

$B_j(x)=\dfrac{\dfrac{p_x}{1-p_x}}{\dfrac{p_0}{1-p_0}}$ $=\dfrac{\dfrac{1}{\dfrac{(1-p_0)}{p_0}\dfrac{\beta(a+x,b+n-x)}{(1/2)^n\beta(a,b)}}}{\dfrac{p_0}{(1-p_0)}}$ $=\dfrac{(1/2)^n\beta(a,b)}{\beta(a+x,b+n-x)}$.

Note que, nesse caso, $BF(x)$ não depende da probabilidade a priori $p_0$ da hipótese $H_0$.

theta0=1/2
n=6; p=1/2
a=1;b=1
x=seq(0,n)
# Fator de Bayes para cada x
BF=(theta0^x)*((1-theta0)^(n-x))*beta(a,b)/beta(a+x,b+n-x)
# Probabilidade a posteriori para cada x
PP=(1 + (((1-p)*beta(a+x,b+n-x))/(p*(theta0^x)*((1-theta0)^(n-x))*beta(a,b)))  )^(-1)
tab=t(tibble(BF=round(BF,4),PP=round(PP,4)))
colnames(tab)=x
kable(tab, booktabs=TRUE, escape=FALSE)

	0	1	2	3	4	5	6
BF	0.1094	0.6562	1.6406	2.1875	1.6406	0.6562	0.1094
PP	0.0986	0.3962	0.6213	0.6863	0.6213	0.3962	0.0986

Na tabela acima, são calculados $P(\theta=1/2|x)$ e $BF(x)$ para cada $x$ com $n=6$, $p_0=1/2$ e os parâmetros da Beta sendo $a=b=1$. Considerando $a_0=b_0=0$ e $a_1=b_1=1$, os valores de corte para a probabilidade a posteriori e o $BF$ são, respectivamente, $1/2$ e $1$. Desta forma, rejeita-se a hipótese nula para os valores “extremos” $\left\{0,1,5,6\right\}$.

$~$

6.7 Hipóteses Precisas

Probabilidade a posteriori da hipótese $H_0$, $P(\Theta_0|\boldsymbol x)$.
Fator de Bayes $BF(\boldsymbol x)$.
No caso absolutamente contínuo, quando $H_0$ é hipótese precisa, $P(\Theta_0|\boldsymbol x)=0$. Isso faz com que os testes anteriores sempre levem à rejeição de $H_0$.
Primeira alternativa: teste de Jeffreys. Problema: a priori deve dar probabilidade positiva à hipótese nula, conduzindo assim a uma priori “artificial” (mista).
Serão apresentados dois procedimentos alternativos de teste: FBST e P-value. O primeiro deles foi pensado especificamente para hipóteses precisas $\left(dim(\Theta_0)<dim(\Theta)\right)$ mas ambos podem ser aplicados para hipóteses gerais.

$~$

6.8 FBST - Full Bayesian Significance Test

Essa solução foi apresentada por Pereira e Stern em 1999. Suponha que o objetivo é testar $H_0:\theta\in\Theta_0$ contra $H_1:\theta \in \Theta_1=\Theta_0^c$. Seja $T_x=\left\{\theta\in\Theta ~:~f(\theta|\boldsymbol x)\geq \underset{\theta\in\Theta_0}{sup}f(\theta|\boldsymbol x)\right\}$ a região tangente à hipóteses $H_0$, formada pelos pontos densidade posterior maior ou igual que qualquer ponto da hipótese nula. Se esse conjunto é “grande” (muito provável), a hipótese nula está em uma região de pouca densidade posterior e deve ser rejeitada. Assim, a medida de evidência (de Pereira-Stern) ou e-value é definido por $Ev(\Theta_0,\boldsymbol x)$ $=1-P\left(\theta\in T_x \big|\boldsymbol x \right)$, e deve-se rejeitar $H_0$ se o e-value for “pequeno.”

$~$

Exemplo. $X_1,...,X_n$ c.i.i.d. $N(\theta,{\sigma}_0^2)$, com ${\sigma}_0^2$ conhecido. Novamente, considere $\theta\sim N(m,v^2)$, de modo que $\theta|\boldsymbol x \sim N\left(\dfrac{{\sigma}_0^2m+nv^2\bar{x}}{{\sigma}_0^2+nv^2},\dfrac{{\sigma}_0^2v^2}{{\sigma}_0^2+nv^2}\right)$ e denote a média e a variância da posteriori por $M_x$ e $V_x$, respectivamente. Suponha que o interesse é testar $H_0:\theta=\theta_0$ contra $H_1:\theta\neq\theta_0$.

Sem perda de generalidade, suponha que $M_x \geq \theta_0$. Então, como a normal é simétrica em torno de $M_x$, a região tangente é da forma $T_x=[\theta_0,2M_x-\theta_0]$.

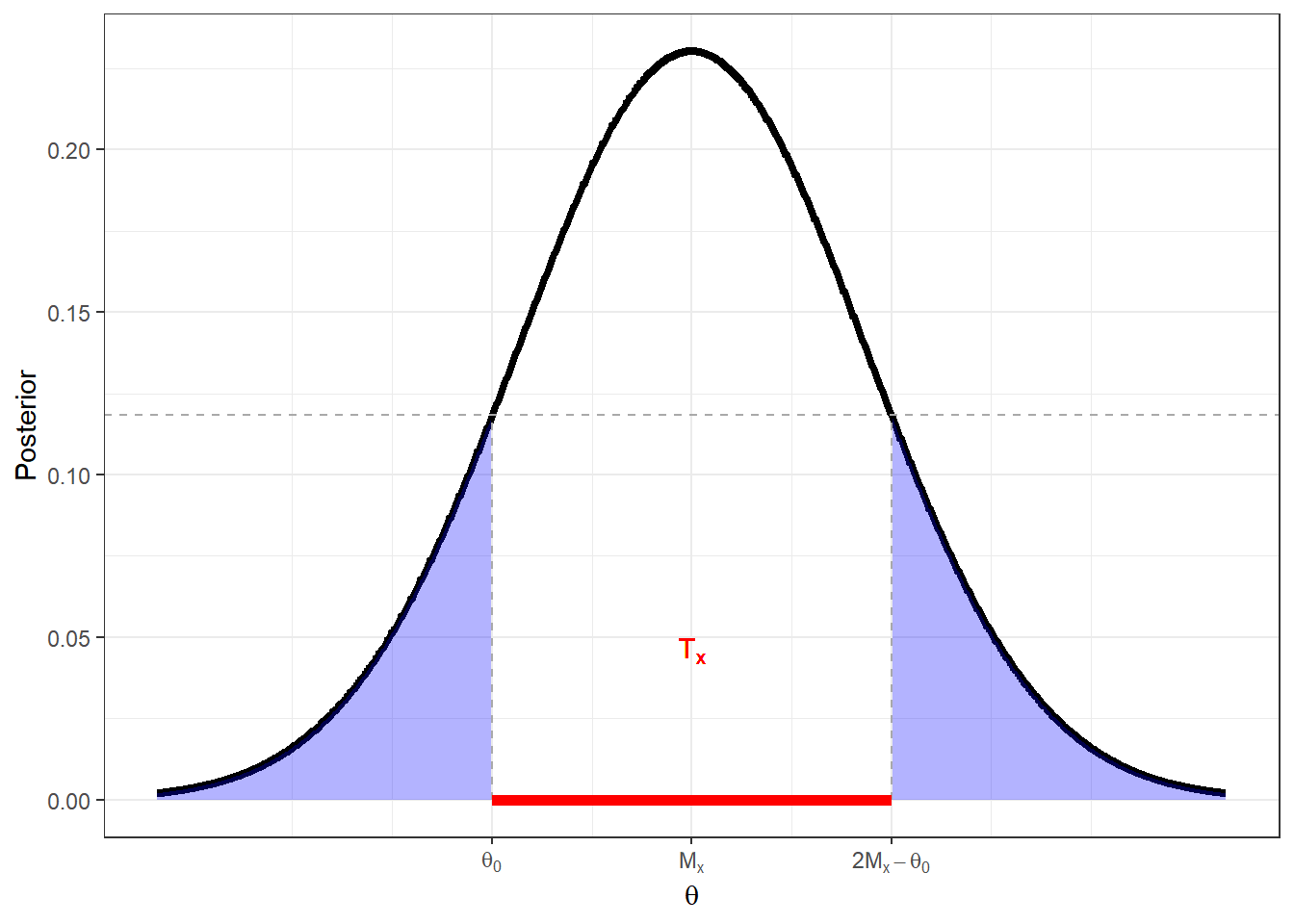
Note que quanto mais próximo $M_x$ está de $\theta_0$, menor a região $T_x$ e, portanto, maior o valor da evidência em favor de $H_0$. O valor da evidência pode ser calculado por

$Ev(\Theta_0,x)=$ $1-P\left(\theta_0\leq \theta\leq2M-\theta_0|x\right)=$ $1-P\left(\dfrac{\theta_0-M}{\sqrt V}\leq Z\leq \dfrac{2M-\theta_0-M}{\sqrt V}|x\right)=$ $2\Phi\left(-\dfrac{|\theta_0-M|}{\sqrt V}\right)=$ $2\Phi\left(-\dfrac{\left|\dfrac{{\sigma}_0^2m+nv^2\bar{x}}{{\sigma}_0^2+nv^2}-\theta_0\right|}{\dfrac{{\sigma}_0 v}{\sqrt{{\sigma}_0^2+nv^2}}}\right)=$ $2\Phi\left(-\dfrac{\sqrt{{\sigma}_0^2+nv^2}}{{\sigma}_0 v}\dfrac{|{\sigma}_0^2(m-\theta_0)+nv^2(\bar x-\theta_0)|}{\sqrt{{\sigma}_0^2+nv^2}}\right)=$ $2\Phi\left(-\dfrac{1}{\sqrt{{\sigma}_0^2+nv^2}}\left|\dfrac{{\sigma}_0}{v}(m-\theta_0)+\dfrac{\sqrt n v}{{\sigma}_0}(\bar x-\theta_0)\right|\right)=$ $2\Phi\left(-\dfrac{1}{\sqrt{{\sigma}_0^2+nv^2}}\left|\dfrac{(m-\theta_0)}{v/{\sigma}_0}+\sqrt nv\dfrac{(\bar x-\theta_0)}{{\sigma}_0/\sqrt n}\right|\right)$

$~$

Sob a abordagem frequentista, temos que o p-value é

$p(\boldsymbol x)$ $= 1-P\left(-\dfrac{|\bar X-\theta_0|}{{\sigma}_0/\sqrt n}\leq Z \leq \dfrac{|\bar X-\theta_0|}{{\sigma}_0/\sqrt n}\right)$ $=2\Phi\left(-\dfrac{|\bar X-\theta_0|}{{\sigma}_0/\sqrt n}\right)$ $\Longleftrightarrow -\dfrac{|\bar X-\theta_0|}{{\sigma}_0/\sqrt n}=\Phi^{-1}\left(\dfrac{p-valor}{2}\right)$,

de modo que, nesse exemplo, podemos escrever

$Ev(\Theta_0,x)=$ $2\Phi\left(-\dfrac{1}{\sqrt{{\sigma}_0^2+nv^2}}~\left|\dfrac{(m-\theta_0)}{v/{\sigma}_0}+\sqrt nv~\Phi\left(\dfrac{p(\boldsymbol x)}{2}\right)\right|\right)$.

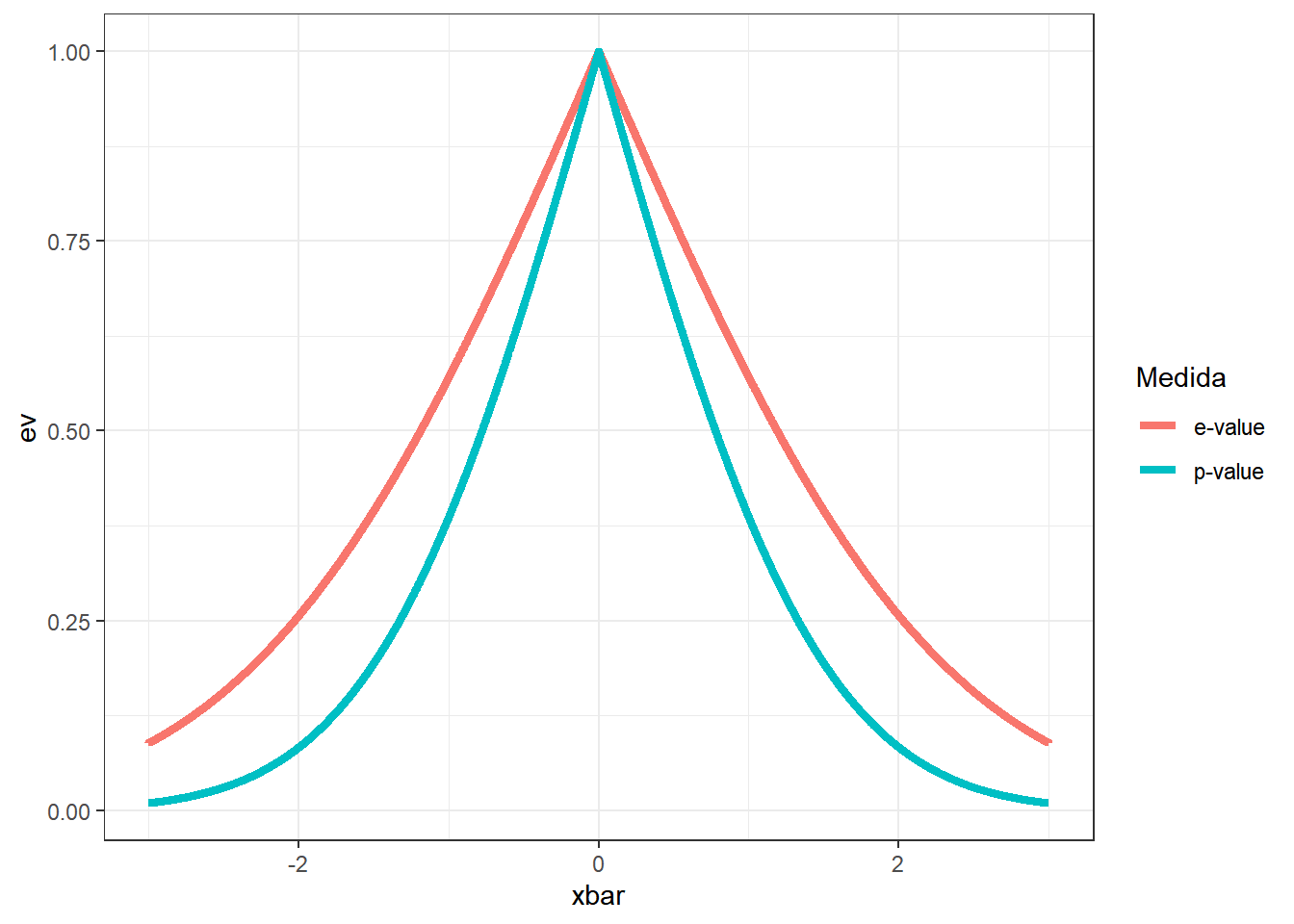
A seguir, são apresentados gráficos do e-value e do p-value como função de $\bar{x}$ e do e-value como função do p-value usando da relação anterior.

sigma02=4
m=0; v2=1
theta0 = 0
n=3
p=seq(0,1,length.out=5000)
ep =  function(p){
  2*pnorm(-abs(sqrt(sigma02/v2)*(m-theta0) + sqrt(n*v2)*qnorm(p/2))/ sqrt(sigma02+n*v2))
}
graf=tibble(pv=p,ev=ep(p)) %>%
  ggplot() +
  geom_line(aes(x=pv,y=ev),lwd=1.5) +
  geom_segment(x=0.05,xend=0.05,y=0,yend=round(ep(0.05),2),lty=2) +
  geom_segment(x=0,xend=0.05,y=round(ep(0.05),2),yend=round(ep(0.05),2),lty=2) +
  scale_y_continuous(breaks=c(0.00,round(ep(0.05),2),0.25,0.50,0.75,1.00)) +
  scale_x_continuous(breaks=c(0.00,0.05,0.25,0.50,0.75,1.00)) +
  theme_bw()
if(knitr::is_latex_output()){
  graf
} else { plotly::ggplotly(graf) }

Suponha que um estatístico frequentista decida rejeitar $H_0$ se o p-value for menor que 0.05. Para que a decisão baseada no e-value concorde com o resultado frequentista (para esse particular exemplo), deve-se rejeitar a hipótese se o e-value for menor que 0.2, aproximadamente. Quando a variância da priori ou o tamanho amostral aumentam, os valores dessas duas medidas se aproximam.

$~$

Resultados Assintóticos (para esse exemplo)

Suponha que $H_0: \theta=\theta_0$ seja falso, isto é, o “verdadeiro” valor do parâmetro é $\theta^* \neq \theta_0$. Quando $n\uparrow\infty$, pela Lei dos Grandes Números,

$\bar{X} ~\overset{q.c.}{\longrightarrow}~ \theta^*$ $~\Longrightarrow~ \dfrac{\sqrt{n}|\bar{X}-\theta_0|}{{\sigma}_0} ~{\longrightarrow}~ +\infty$ $~\Longrightarrow~ p(\boldsymbol X)= 2\Phi\left(-\dfrac{\sqrt{n}|\bar{X}-\theta_0|}{{\sigma}_0}\right) ~{\longrightarrow}~ 0$,

com probabilidade 1. Por outro lado, sob $H_0: \theta=\theta_0$, pelo Teorema Central do Limite,

$\dfrac{\sqrt{n}(\bar{X}-\theta_0)}{{\sigma}_0} ~\overset{\mathcal{D}}\longrightarrow~ Z \sim N(0,1)$ $~\Longrightarrow~ p(\boldsymbol X)= 2\Phi\left(-\dfrac{\sqrt{n}|\bar{X}-\theta_0|}{{\sigma}_0}\right) ~\overset{\mathcal{D}}\longrightarrow~ U=2\Phi\left(-|Z|\right) \sim Unif(0,1)$.

$~$

Esses resultados para o p-value são bastante conhecidos. No contexto desse exemplo, é possível obter resultados similares para o e-value. Novamente, considere que $H_0$ é falso e, sem perda de generalidade, $\theta=\theta^*>\theta_0$. Note que

$\dfrac{{\sigma}_0(m-\theta_0)}{v\sqrt{{\sigma}_0^2+nv^2}} ~\longrightarrow~ 0$

e, pela LGN,

$\bar{X} ~\overset{q.c.}{\longrightarrow}~ \theta^*$ $~\Longrightarrow~ (\bar{X}-\theta_0) ~{\longrightarrow}~ (\theta^*-\theta_0) >0$ $~\Longrightarrow~ \dfrac{nv(\bar{X}-\theta_0)}{{\sigma}_0^2\sqrt{{\sigma}_0^2+nv^2}} ~{\longrightarrow}~ +\infty$ $~\Longrightarrow~ Ev(\Theta_0,\boldsymbol X)=2\Phi\left(-\left|\dfrac{{\sigma}_0(m-\theta_0)}{v{\sqrt{{\sigma}_0^2+nv^2}}}+\dfrac{nv(\bar x-\theta_0)}{{\sigma}_0{\sqrt{{\sigma}_0^2+nv^2}}}\right|\right) ~{\longrightarrow}~ 2\Phi\left(-\infty\right)=0$.

Além disso, $\dfrac{v\sqrt{n}}{\sqrt{{\sigma}_0^2+nv^2}} ~\longrightarrow~ 1$ e, sob $H_0: \theta = \theta_0$,

$\dfrac{v\sqrt{n}}{\sqrt{{\sigma}_0^2+nv^2}}\dfrac{\sqrt{n}(\bar{X}-\theta_0)}{{\sigma}_0} ~\overset{\mathcal{D}}\longrightarrow~ Z \sim N(0,1)$,

de modo que

$Ev(\Theta_0,\boldsymbol{X})=2\Phi\left(-\left|\dfrac{{\sigma}_0(m-\theta_0)}{v{\sqrt{{\sigma}_0^2+nv^2}}}+\dfrac{nv(\bar x-\theta_0)}{{\sigma}_0{\sqrt{{\sigma}_0^2+nv^2}}}\right|\right) ~{\longrightarrow}~ 2\Phi\left(-|Z|\right)\sim Unif(0,1)$.

Esse resultado pode não valer em outros contextos. Por exemplo, quando $dim(\Theta_0)\geq 2$, a distribuição de $Ev(\Theta_0,\boldsymbol{X})$ sob $H_0$ não é $Unif(0,1)$, em geral.

$~$

6.9 P-value - Nível de Significância Adaptativo

Recentemente, o p-value e a utilização do famoso nível $\alpha=0.05$ têm sido muito questionados, não apenas na área de testes de hipóteses mas na ciência como um todo. A ideia de fixar um nível de significância é que a probabilidade de erro tipo I fica “controlada” e a probabilidade do erro tipo II diminui quanto maior o tamanho amostral. Por essa razão, é comum nas áreas de planejamento de experimentos e amostragem, o cálculo do tamanho amostral para um determinado estudo. Infelizmente, na maior parte dos problemas do dia a dia de um estatístico, não há um planejamento cuidadoso ou as amostras disponíveis são “amostras de conveniência.” Simultaneamente, com a “revolução da informação,” a quantidade de dados disponível é cada vez maior. A consequência disso no cenário de testes de hipóteses é que os testes ficam muito poderosos e há uma tendência maior de rejeitar a hipótese nula.

$~$

Exemplo. Seja $X_1,\ldots,X_n$ c.i.i.d. tais que $X_i|\theta \sim Ber(\theta)$, $\theta \sim Beta(a,b)$ de modo que $\theta|x=\sum x_i \sim Beta(a+x,b+n-x)$ e suponha que deseja-se testar $H_0: \theta= 1/2$. A seguir, para diferentes tamanhos amostrais $n$ e supondo que em todos os casos $\bar{x}_n=0.55$, são apresentados os testes para esse caso vistos até aqui: p-value do teste RVG, probabilidade posterior e $BF$ do teste de Jeffreys e e-value do FBST.

a=1; b=1
p=0.5
alpha=0.05
theta0=0.5
xbar=0.55
N=c(1,5,10,20,30,40,50,100,150,300,seq(500,2000,250))
p_v=Vectorize(function(n){
  x=n*xbar
  l = c(min(x,n-x),max(x,n-x))
  pbinom(l[1],n,theta0) + 1-pbinom(l[2],n,theta0) })
Nalpha=seq(max(N[(p_v(N)-alpha)>0]),min(N[(p_v(N)-alpha)<0]))
Nalpha=Nalpha[which.min(abs(p_v(Nalpha)-alpha))]
bf=Vectorize(function(n){
  x=n*xbar
  # exp(log(BF))
  exp(x*log(theta0) + (n-x)*log(1-theta0) + lbeta(a,b) - lbeta(a+x,b+n-x)) })
prob_post=Vectorize(function(n){
  x=n*xbar
  l = log(1-p)+lbeta(a+x,b+n-x)-log(p)-x*log(theta0)-(n-x)*log(1-theta0)-lbeta(a,b)
  1/(1+exp(l)) })
e_v=Vectorize(function(n){
  x=n*xbar
  f_Tx=function(t){ dbeta(t,a+x,b+n-x)-dbeta(theta0,a+x,b+n-x) }
  moda=(a+x-1)/(a+b+n-2)
  if(theta0==moda){ return(1) }
  if(theta0<moda){
    Tx=c(theta0,uniroot(f=f_Tx,lower=moda,upper=1)$root)
  }else{
    Tx=c(uniroot(f=f_Tx,lower=0,upper=moda)$root,theta0)
  }
  pbeta(Tx[1],a+x,b+n-x)+1-pbeta(Tx[2],a+x,b+n-x)
})
Dados=tibble(n=rep(N,4), Evidencia=c(p_v(N),prob_post(N),bf(N),e_v(N)),
       Estatistica=factor(rep(c("p-value","Prob. Post.","BF","e-value"),
          each=length(N)),levels=c("Prob. Post.","BF","e-value","p-value")),
       corte=c(p_v(Nalpha),rep(NA,4*length(N)-1)))
ggplot(Dados)+
  geom_line(aes(x=n,y=Evidencia, colour=Estatistica),lwd=1.5)+
  geom_vline(xintercept=Nalpha,lty=2,col="darkgrey")+
  facet_wrap(~Estatistica, scales="free_y")+
  geom_hline(data=subset(Dados,Estatística="p-value"),aes(yintercept=corte), lty=2, col="darkgrey")+
  theme_bw()

Note que todas as medidas de suporte da hipótese tendem a zero conforme aumenta o tamanho amostral. Isso indica que se $|\bar{x}_n-\theta_0|=\varepsilon$ e for fixado um valor de corte para essas medidas que não dependa do tamanho amostral (por exemplo, o $\alpha=0.05$ para o p-value), existe um $n^*$ tal que $H_0$ será rejeitado para todo $n\geq n^*$. No gráfico, a linha vertical tracejada indica o valor $n^*$ para o p-value considerando o corte $\alpha=0.05$.

$~$

Como visto anteriormente, o Lema de Neyman-Pearson Generalizado (DeGroot, 1986) garante que os testes Bayesianos (baseados na probabilidade posterior ou no BF) minimizam $a\alpha + b\beta$. Baseado nesse resultado, O professor Carlos A. B. Pereira recentemente propôs um novo procedimento de teste para evitar o problema descrito anteriormente.

Seja $BF(\boldsymbol x) = \dfrac{f_0(\boldsymbol x)}{f_1(\boldsymbol x)}$ $=\dfrac{\displaystyle\int_{\Theta_0} f(\boldsymbol x|\theta) dP_0(\theta)}{\displaystyle \int_{\Theta_1} f(\boldsymbol x|\theta) dP_1(\theta)}$, onde $P_i$ é a medida de probabilidade a priori para $\theta$ restrito à hipótese $H_i$, $i=0,1$;
Defina $\alpha_n = P\left(\left\{\boldsymbol x : BF(\boldsymbol x)\leq\dfrac{b}{a}\right\} ~\Big|~ \Theta_0\right)$ e $\beta_n = P\left(\left\{\boldsymbol x : BF(\boldsymbol x)>\dfrac{b}{a}\right\} ~\Big|~ \Theta_1\right)$;
Suponha que foi observado $\boldsymbol X=\boldsymbol x_o$. O P-value é dado por $\text{P-value}(\boldsymbol x_o) = P\left(\left\{\boldsymbol x : BF(\boldsymbol x)\leq BF(\boldsymbol x_o)\right\} ~\Big|~ \Theta_0\right)$;
O procedimento de teste consiste em rejeitar $H_0$ se $\text{P-value}(\boldsymbol x) < \alpha_n$.

$~$

Voltando ao Exemplo. As distribuções preditivas sob $H_0: \theta=\theta_0=1/2$ e $H_1:\theta \neq 1/2$ são

$f_0(\boldsymbol x)$ $= f(\boldsymbol x | \theta_0)$ $=\displaystyle \binom{n}{x} {\theta}_0^x (1-{\theta}_0)^{n-x}$ $=\displaystyle \binom{n}{x} {(1/2)^{n}}$ ;

$f_1(\boldsymbol x)$ $=\displaystyle \int_{\Theta\setminus\theta_0} f(\boldsymbol x|\theta) f(\theta) d\theta$ $=\displaystyle \int_0^1 \binom{n}{x} \dfrac{{\theta}_0^{a+x-1} (1-{\theta}_0)^{b+n-x-1}}{\beta(a,b)}~d\theta$ $=\displaystyle \binom{n}{x}\dfrac{\beta(a+x,b+n-x)}{\beta(a,b)}$ .

Deste modo,

$BF(\boldsymbol x)$ $=\dfrac{f_0(\boldsymbol x)}{f_1(\boldsymbol x)}$ $=\dfrac{\beta(a,b)~{\theta}_0^x (1-{\theta}_0)^{n-x}}{\beta(a+x,b+n-x)}$ $=\dfrac{\beta(a,b)~(1/2)^{n}}{\beta(a+x,b+n-x)}$,

e, assim,

$\alpha_n = \displaystyle {(1/2)^{n}} \sum_{\left\{\boldsymbol x: BF(\boldsymbol x)\leq\frac{b}{a}\right\}}\binom{n}{x}$,

$\beta_n = \displaystyle \dfrac{1}{{\beta(a,b)}} \sum_{\left\{\boldsymbol x: BF(\boldsymbol x)>\frac{b}{a}\right\}}\binom{n}{x}\beta(a+x,b+n-x)$,

$\text{P-value}(\boldsymbol x_0) = \displaystyle {(1/2)^{n}} \sum_{\left\{\boldsymbol x: BF(\boldsymbol x)\leq BF(\boldsymbol x_o)\right\}}\binom{n}{x}$

$~$

Supondo novamente que foi observado $\bar{x}=0.55$, o gráfico abaixo apresenta esses valores para diversos tamanhos amostrais.

a=1; b=1
a1=1; b1=1
p=0.5
alpha=0.05
theta0=0.5
xbar=0.55
N=c(2,5,seq(10,150,10),seq(150,1000,50))
bf=Vectorize(function(x,n){
  exp(x*log(theta0) + (n-x)*log(1-theta0) + lbeta(a,b) - lbeta(a+x,b+n-x))
}, vectorize.args = c("x"))
alphaN = Vectorize(function(n){
  x=n*xbar
  s=seq(0,n)
  s=s[bf(s,n)<=b1/a1]
  (0.5)^n*sum(choose(n,s))
})
betaN = Vectorize(function(n){
  x=n*xbar
  s=seq(0,n)
  s=s[bf(s,n)>b1/a1]
  sum(extraDistr::dbbinom(s,n,a,b))
})
P_v=Vectorize(function(n){
  x=n*xbar
  s=seq(0,n)
  s=s[bf(s,n)<=bf(x,n)]
  (0.5)^n*sum(choose(n,s))
})
Dados=tibble(n=N, alpha=alphaN(N), beta=betaN(N), Pvalue=P_v(N))
ggplot(Dados)+
  geom_line(aes(x=n,y=Pvalue, colour="P-value"),lwd=1.2)+
  geom_line(aes(x=n,y=alpha, colour="alpha"),lwd=1.2)+
  geom_line(aes(x=n,y=beta, colour="beta"),lwd=1.2)+
  geom_line(aes(x=n,y=alpha+beta, colour="alpha+beta"),lwd=1.2)+
  theme_bw() + labs(colour="")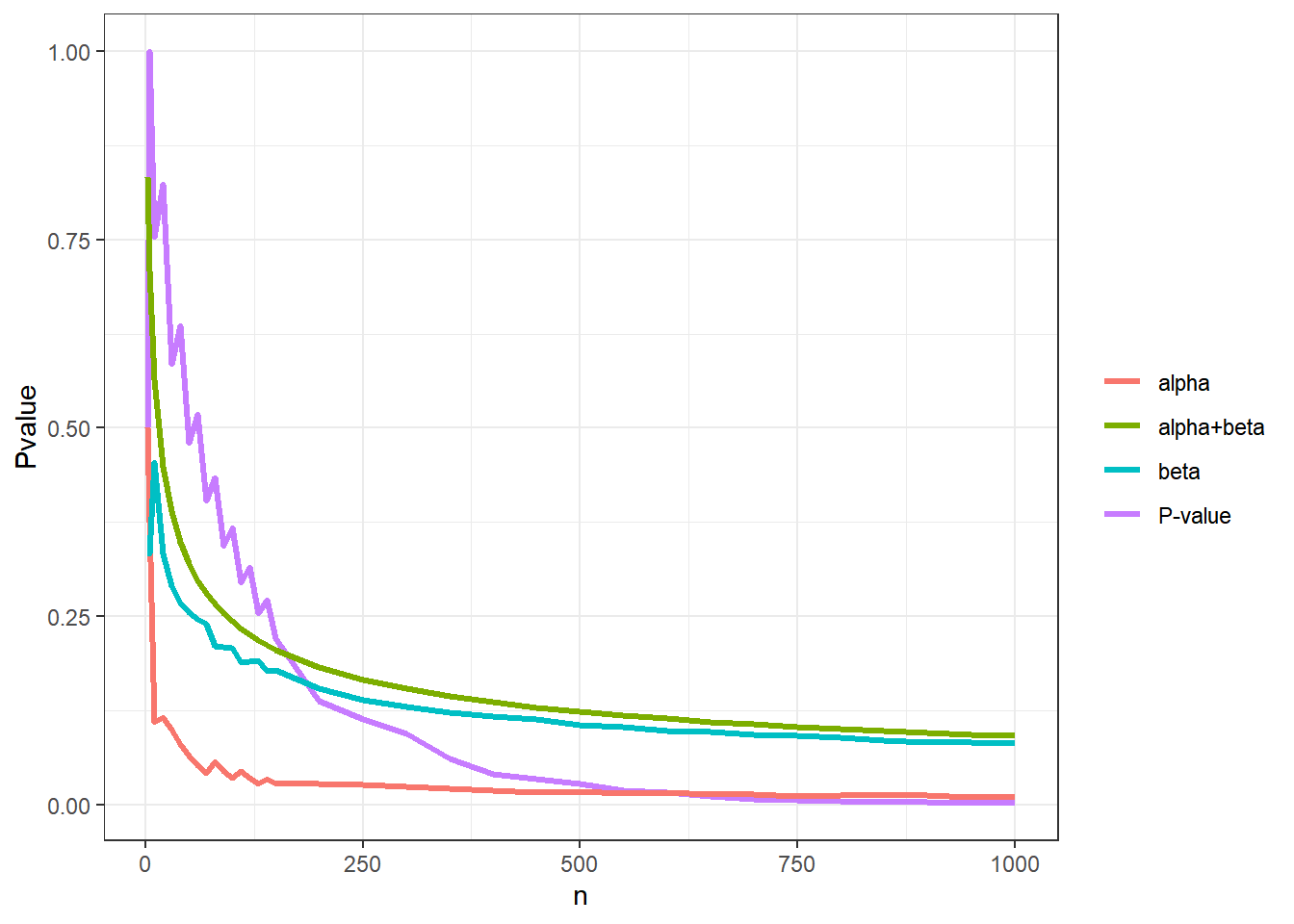

$~$

\(L(d,\theta)\)	\(\theta_0\)	\(\theta_1\)
\(d_0\)	\(0\)	\(b\)
\(d_1\)	\(a\)	\(0\)

\(L(d,\theta)\)	\(\Theta_0\)	\(\Theta_1\)
\(d_0\)	\(a_0\)	\(b_1\)
\(d_1\)	\(a_1\)	\(b_0\)

\(L(d,\theta)\)	\(\Theta_0\)	\(\Theta_1\)
\(d_0\)	\(a_0\)	\(b_1\)
\(d_1\)	\(a_1\)	\(b_0\)

Fundamentos de Inferência Bayesiana