7 Métodos Computacionais

Como visto, a inferência Bayesiana é baseada na aplicação monótona do teorema de Bayes

\(f(\theta|\boldsymbol x)=\dfrac{f(\boldsymbol x|\theta)f(\theta)}{\displaystyle\int_\Theta f(\boldsymbol x|\theta)f(\theta)d\theta}\) \(= c(\boldsymbol x) f(\boldsymbol x|\theta)f(\theta)\) \(\propto f(\boldsymbol x|\theta)f(\theta)\),

e na obtenção de medidas resumo dessa distribuição, como \(E[\theta|\boldsymbol x]\), regiões HPD ou probabilidades a posteriori.

A maior dificuldade na aplicação de Inferência Bayesiana está justamente no cálculo das integrais envolvidas, tanto no cálculo de \(f(\boldsymbol x)\) para a obtenção da posteriori, quanto na obtenção das medidas resumos citadas anteriormente. Devido a isso, a inferência bayesiana ganhou muito força com o avanço computacional das últimas décadas. A seguir, serão apresentados um breve resumo de alguns recursos que podem ser utilizados na prática Bayesiana.

Muitos dos métodos descritos baseiam-se na Lei dos Grande Números (LGN) e são uma bela aplicação de ideias frequentistas em um cenário controlado onde as suposições de i.i.d. são satisfeitas.

\(~\)

Lei \(\overset{\textbf{(Fraca)}}{\textbf{Forte}}\) dos Grande Números. Seja \(X_1,X_2...\) uma sequência de v.a. i.i.d com \(E[X_1]=\mu\) e \(Var[X_1]=\sigma^2<\infty\), então

\(\dfrac{1}{n}\displaystyle \sum_{i=1}^n X_i ~~\underset{q.c.}{\overset{P}{\longrightarrow}}~~ E[X_1]=\mu\).

\(~\)

As integrais de interesse aqui serão escritas como o valor esperado de funções de variáveis aleatórias, isto é,

\(\displaystyle \int g(x) dP(x) = E\left[g(X)\right]\).

Deste modo, suponha que \(X_1,X_2...\) é uma sequência de v.a. i.i.d e \(g:\mathbb{R} \longrightarrow\mathbb{R}\) é uma função (mensurável) tal que \(Var\left[g(X_1)\right]<\infty\). Então, pela LGN,

\(\dfrac{1}{n}\displaystyle \sum_{i=1}^n g(X_i) ~\longrightarrow~ E\left[g(X_1)\right]\)

\(~\)

7.1 Método de Monte Carlo

Suponha que deseja-se calcular \(\displaystyle\int_\Theta g(\theta)f(\theta|\boldsymbol x)d\theta=E\left[g(\theta)|\boldsymbol x\right]\) e é possível simular realizações \(\theta_1,...,\theta_m\) da distribuição de \(\theta |\boldsymbol X=\boldsymbol x\) , \(f(\theta | \boldsymbol x)\).

Então, a integral acima pode ser aproximada por \(\displaystyle \dfrac{1}{m}\sum_{i=1}^m g(\theta_i)\)

A precisão da aproximação é usualmente estimada pelo erro padrão da estimativa
\(\displaystyle EP\left[\dfrac{1}{m}\sum_{i=1}^m g(\theta_i)\right]\) \(\approx \displaystyle \sqrt{\dfrac{1}{m}\left(\dfrac{1}{m}\sum_{i=1}^m\Big[g(\theta_i)\Big]^2-\left[\dfrac{1}{m}\sum_{j=1}^mg(\theta_j)\right]^2\right)}\)

\(~\)

Exemplo 1. Suponha que deseja-se estimar o número \(\pi\) usando o método de Monte Carlo. Considere então que o v.a. \((X,Y)\) tem distribuição uniforme em um quadrado centrado na origem, \(\mathfrak{X}=[-1,1]\times[-1,1]\), e um círculo \(A\) de raio \(1\) inscrito nesse quadrado, \(x^2+y^2\leq 1.\) Como a distribuição é uniforme no quadrado, a probabilidade de escolher um ponto no círculo é
\(P(A)\) \(=\dfrac{\text{área da círculo}}{\text{área do quadrado}}\) \(=\dfrac{\pi}{4}\) \(= \displaystyle\int_A f(x,y) dxdy\) \(= \displaystyle\int_{\mathfrak{X}} \mathbb{I}_A(x,y)~\dfrac{1}{4}~dxdy\) \(=E\left[\mathbb{I}_A(X,Y)\right]~.\)
Suponha que é possível gerar uma amostra \(\left\{(x_1,y_1),\ldots,(x_m,y_m)\right\}\) de \((X,Y)\), de modo que podemos aproximar o valor de \(\pi\) por
\(\pi\) \(=4~P(A)\) \(=E\left[4~\mathbb{I}_A(X,Y)\right]\) \(\displaystyle \approx \dfrac{1}{m}\sum_{i=1}^m 4~\mathbb{I}_A(x_i,y_i)\),
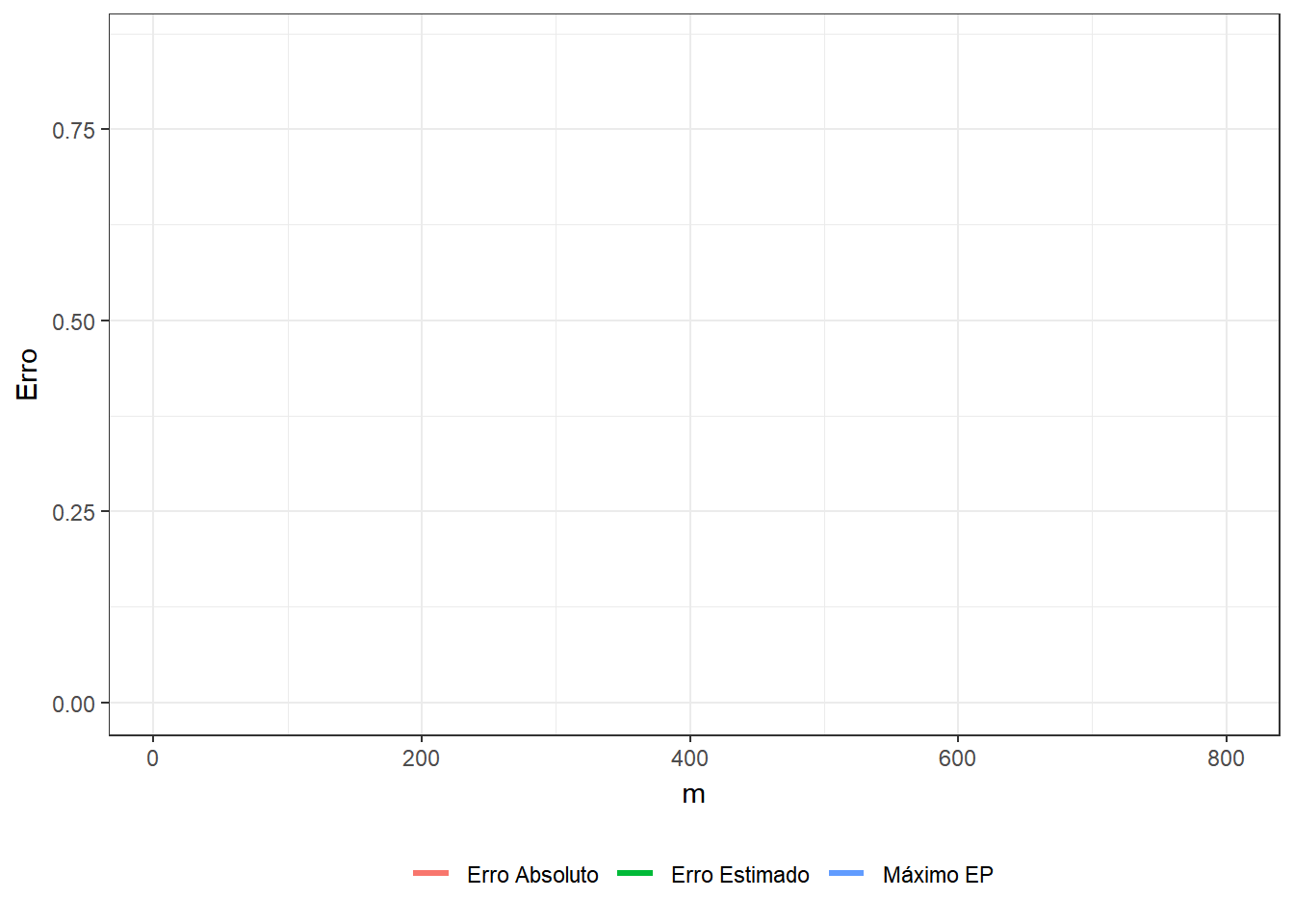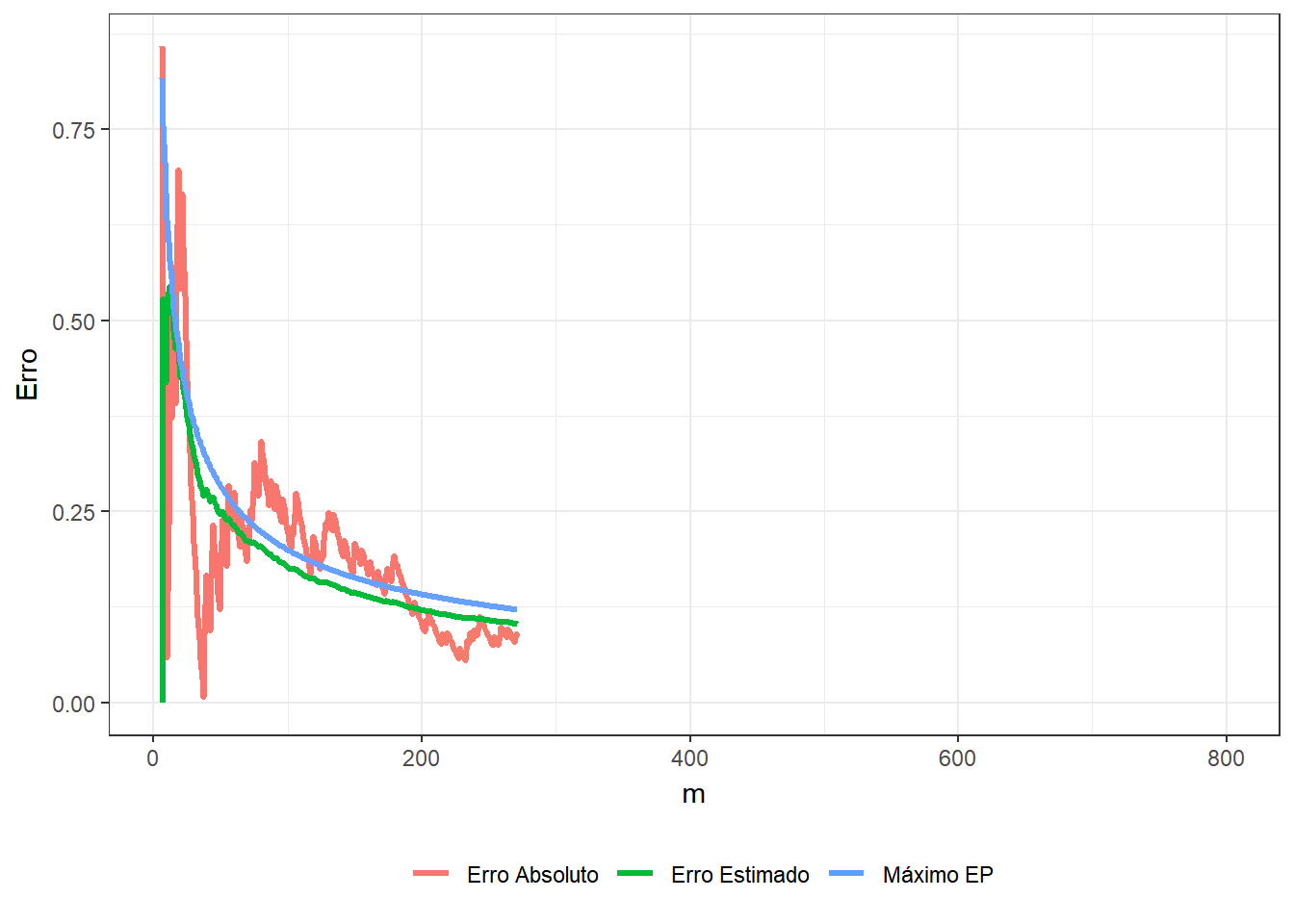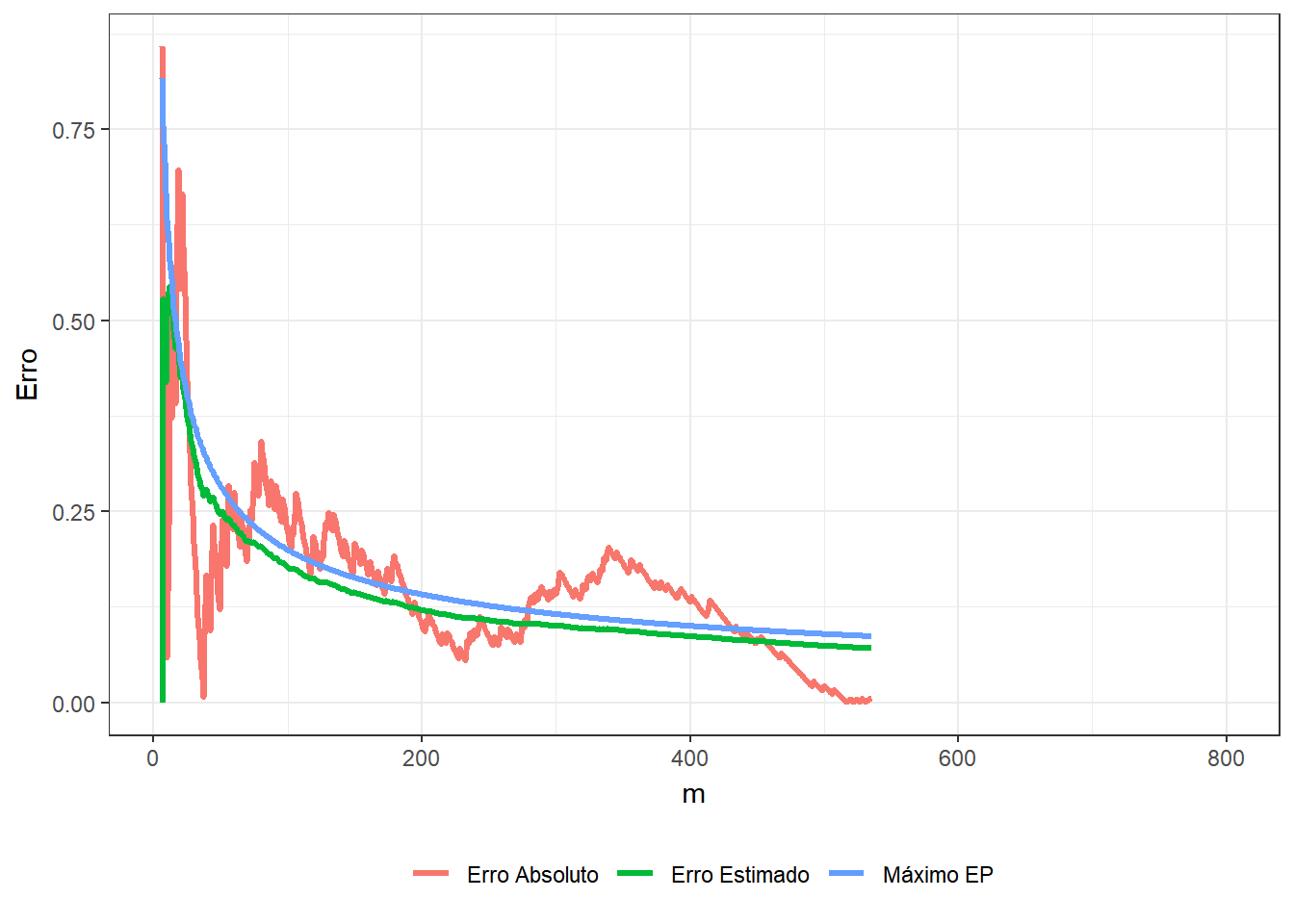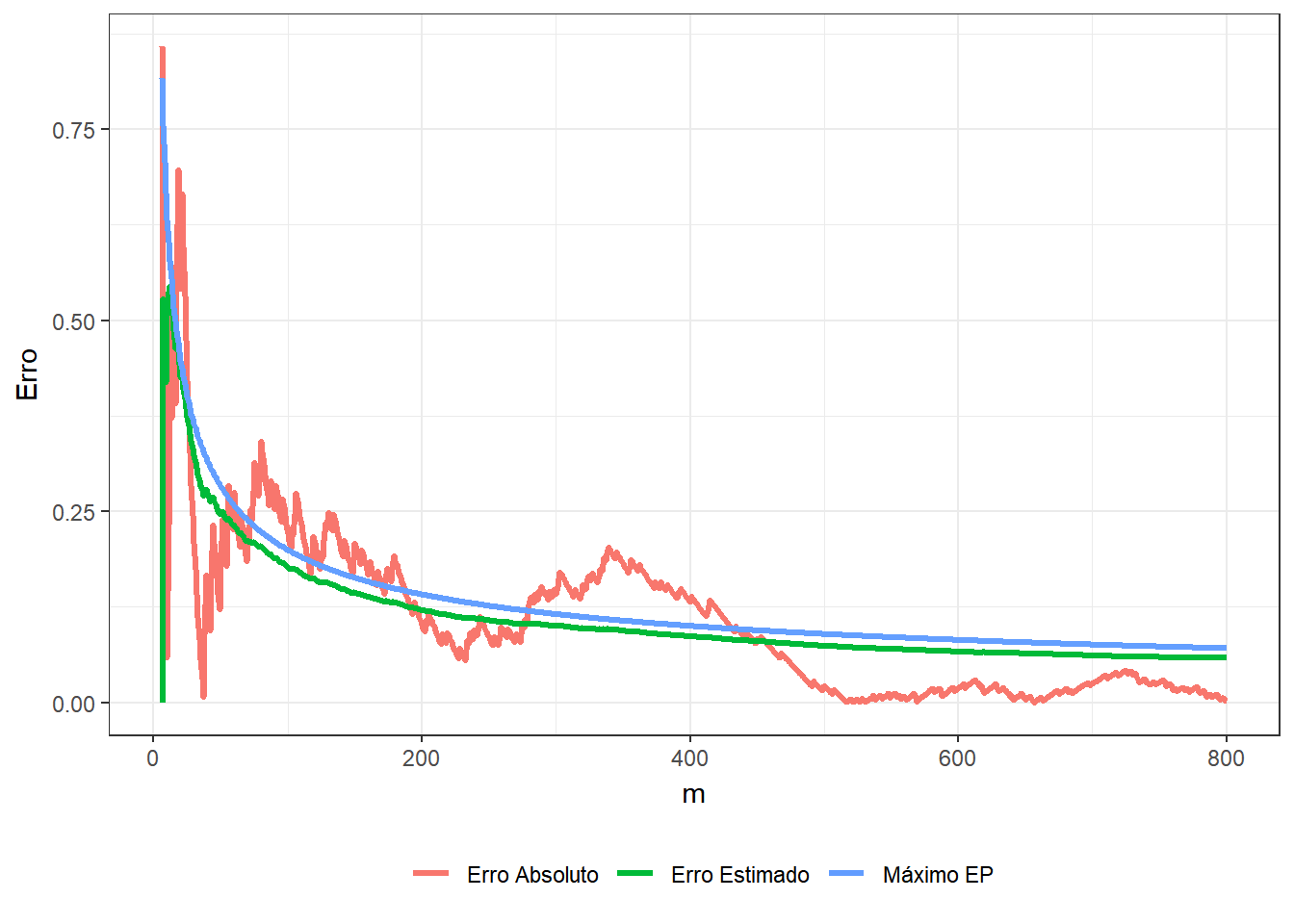
e, denotando por \(\displaystyle t=\sum_{i=1}^m ~\mathbb{I}_A(x_i,y_i)\), o erro estimado é
\(\displaystyle \sqrt{\dfrac{1}{m}\left(\dfrac{1}{m}\sum_{i=1}^m\Big[4~\mathbb{I}(x_i,y_i)\Big]^2-\left[\dfrac{1}{m}\sum_{j=1}^m 4~\mathbb{I}(x_i,y_i)\right]^2\right)}\) \(=\displaystyle \sqrt{\dfrac{1}{m}\left(\dfrac{16}{m}~t-\left[\dfrac{4}{m}~t\right]^2\right)}\) \(= \displaystyle \sqrt{\dfrac{16}{m} \dfrac{t}{m}\left(1-\dfrac{t}{m}\right)}\) \(\leq \displaystyle \sqrt{\dfrac{16}{m}~\dfrac{1}{4}}\) \(= \dfrac{2}{\sqrt{m}}~.\)

set.seed(666)
M = 1000 # número de iterações
df = tibble(t = 1:M, x = runif(length(t), -1, 1), 
            y = runif(length(t), -1, 1)) %>% 
  mutate(Circ=ifelse(x^2+y^2<=1,1,0), 
         pi_est=round(4*cumsum(Circ)/t,4),
         erro=round(abs(pi-pi_est),4),
         erro_est=round(sqrt((cumsum(16*Circ)/t-pi_est^2)/t),4))
p <- ggplot() + theme_bw() + 
        theme(panel.grid.major = element_blank(),
            panel.grid.minor = element_blank(),
            panel.border = element_blank(),
            panel.background = element_blank()) +
        ggforce::geom_circle(aes(x0 = 0, y0 = 0, r = 1), color = "black") +
        geom_rect(aes(xmin = -1, ymin = -1, xmax = 1, ymax = 1), 
                  color = "black", alpha = 0) + 
        guides(color = FALSE) +
        geom_point(data = df, aes(x = x, y = y, colour = Circ), size = 3) + 
        gganimate::transition_manual(t, cumulative = TRUE) 
p + labs(title = expression(paste("Método de Monte-Carlo para a estimação do ",pi)), subtitle = "m = {df$t[frame]}  ;   pi_est = 4 * ({cumsum(df$Circ)[frame]} / {df$t[frame]}) = {df$pi_est[frame]}  ;   erro = {df$erro[frame]}  ;   erro_est = {df$erro_est[frame]}")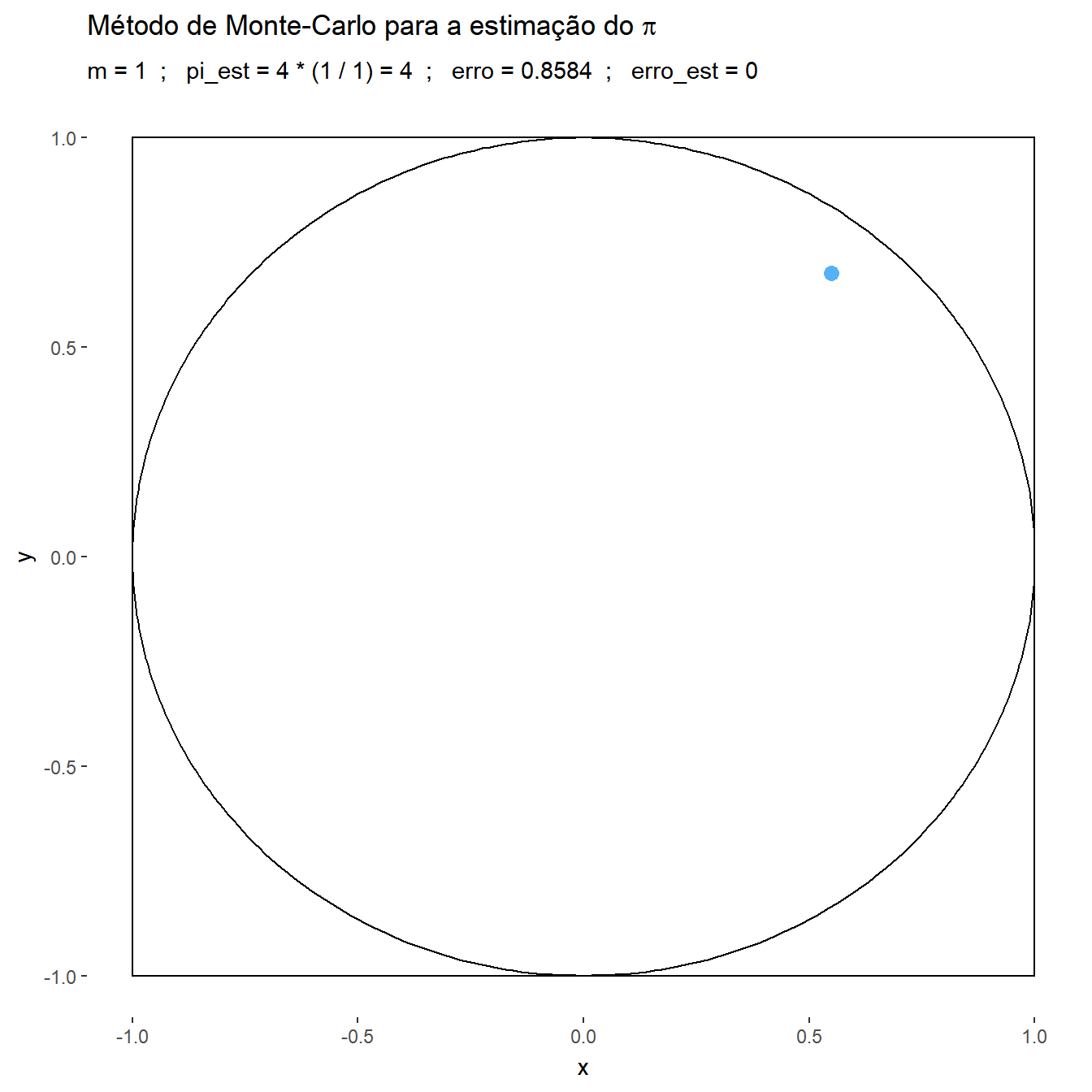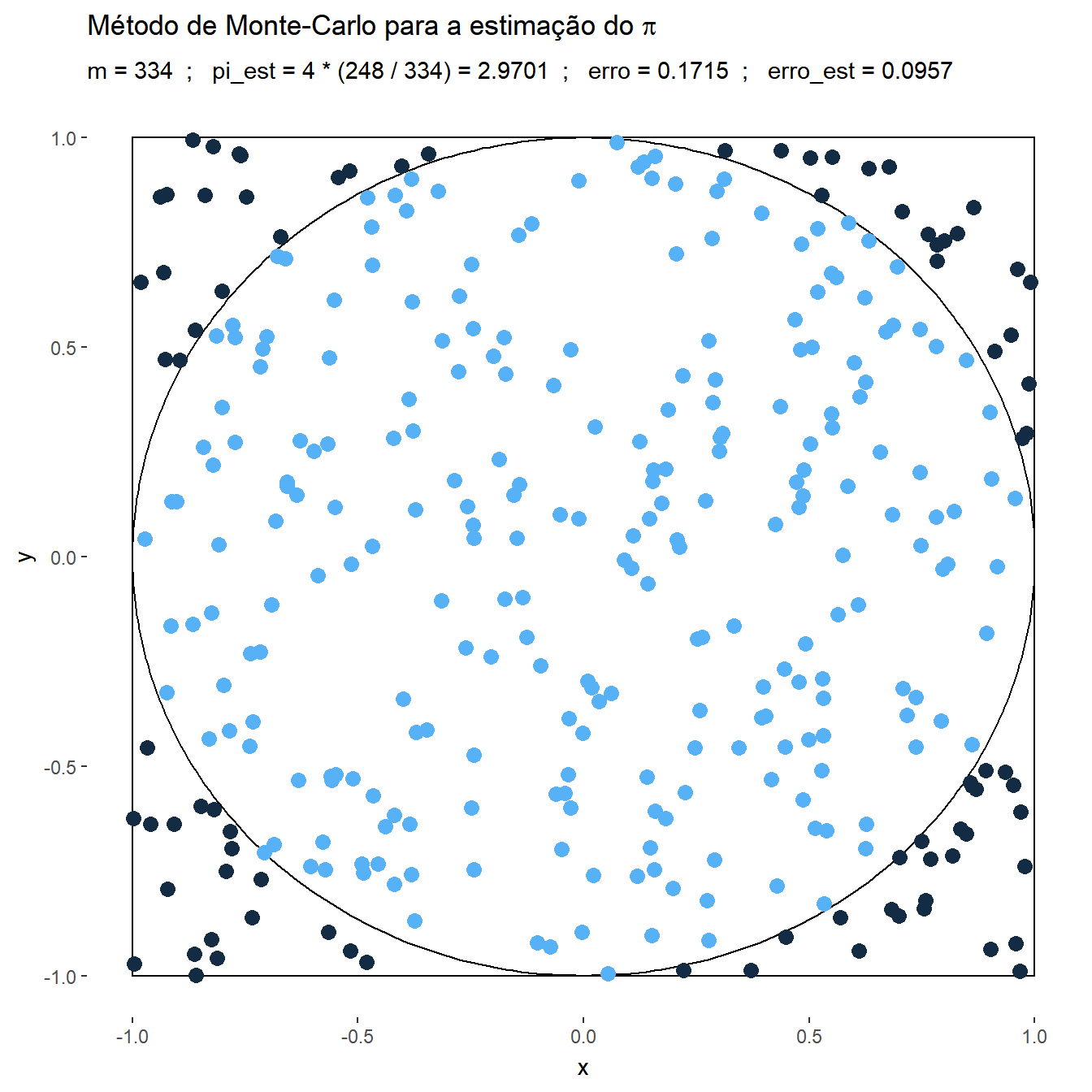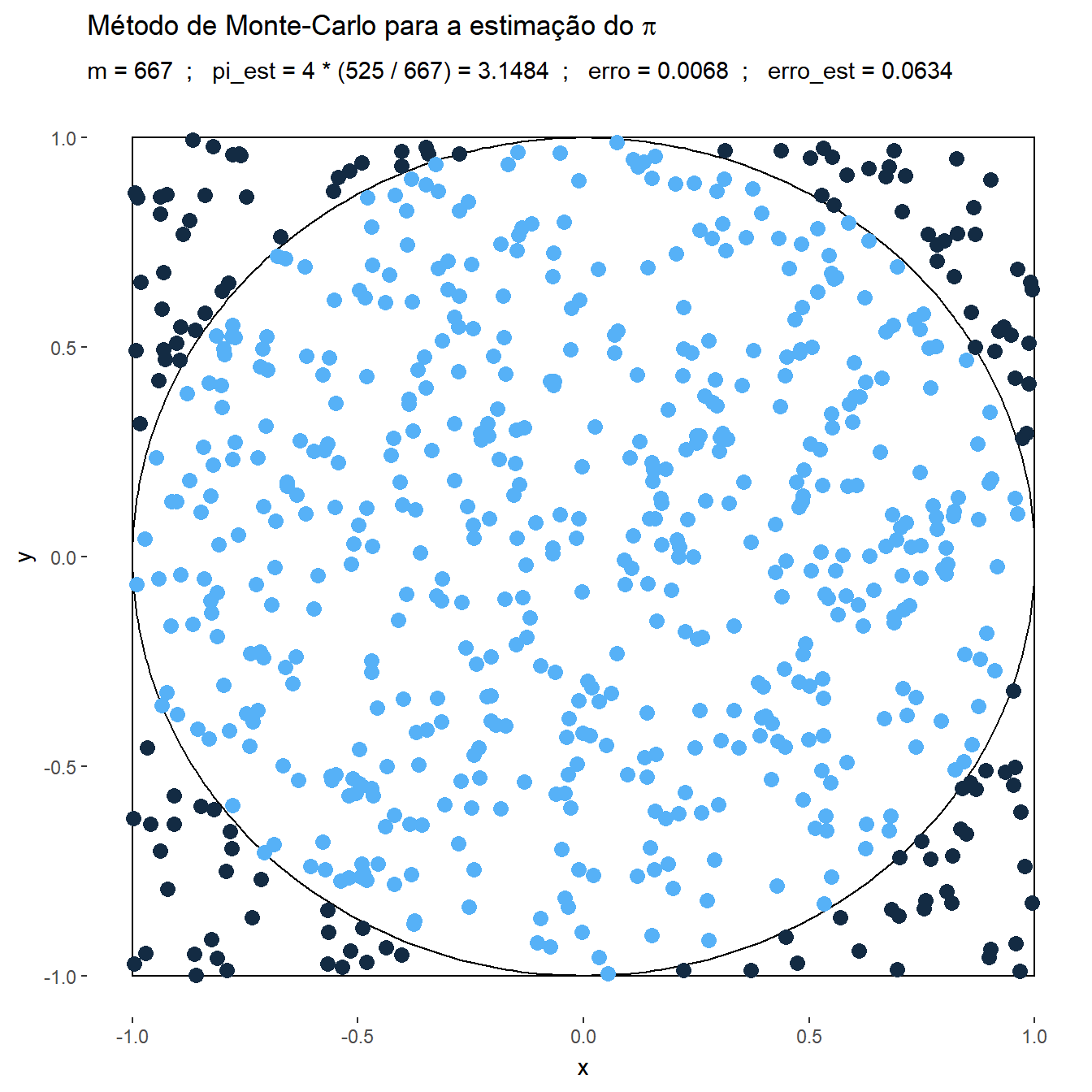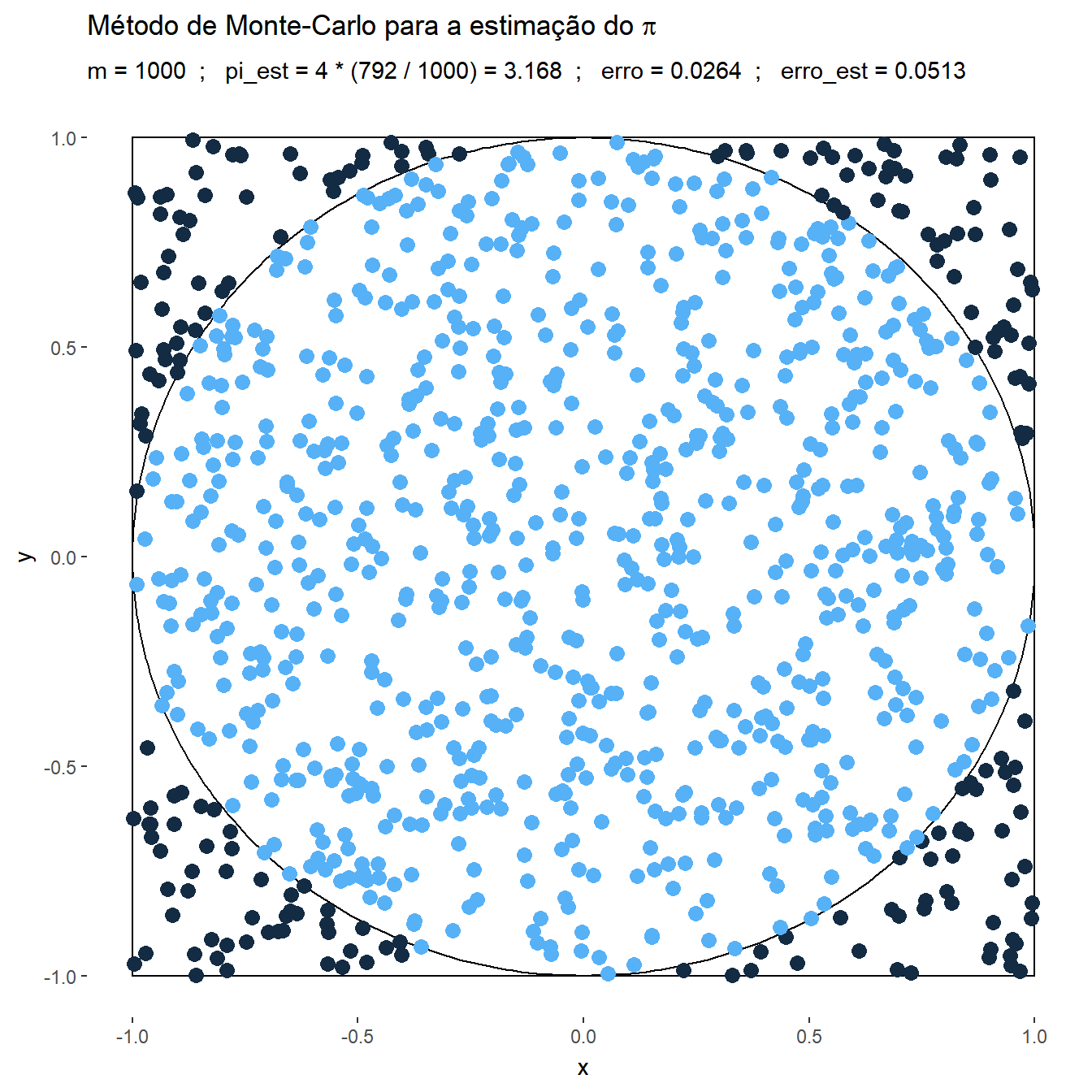

\(~\)

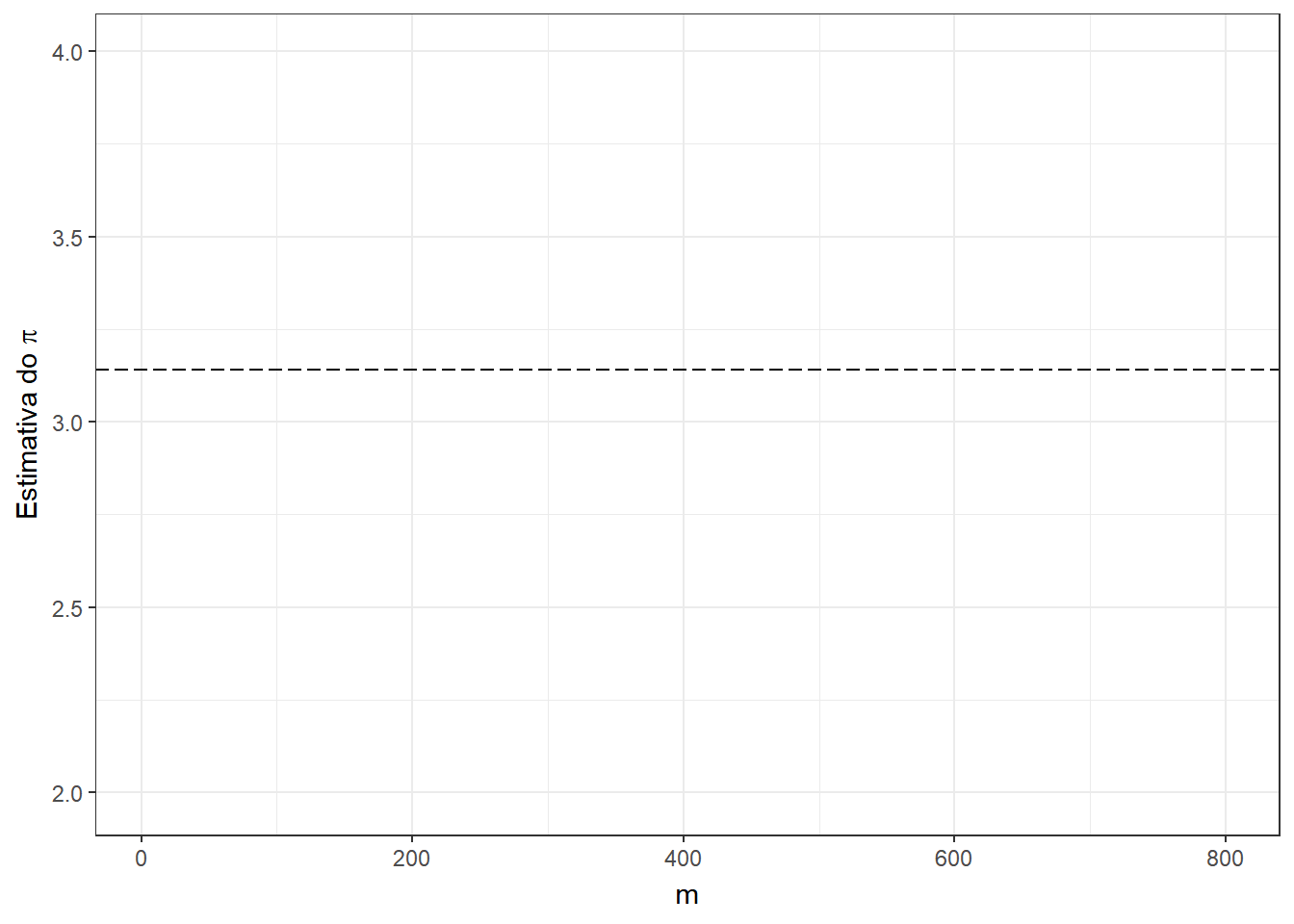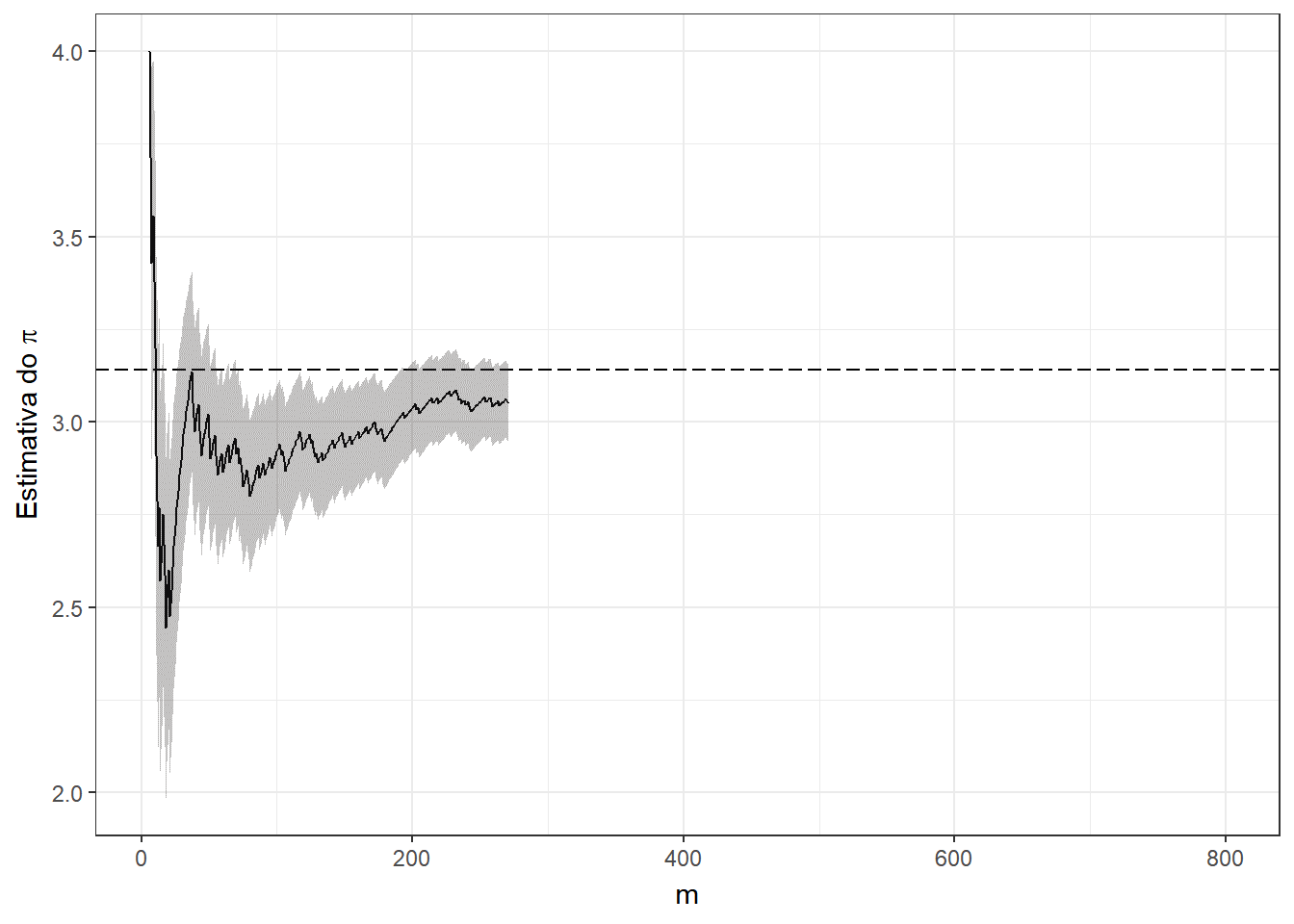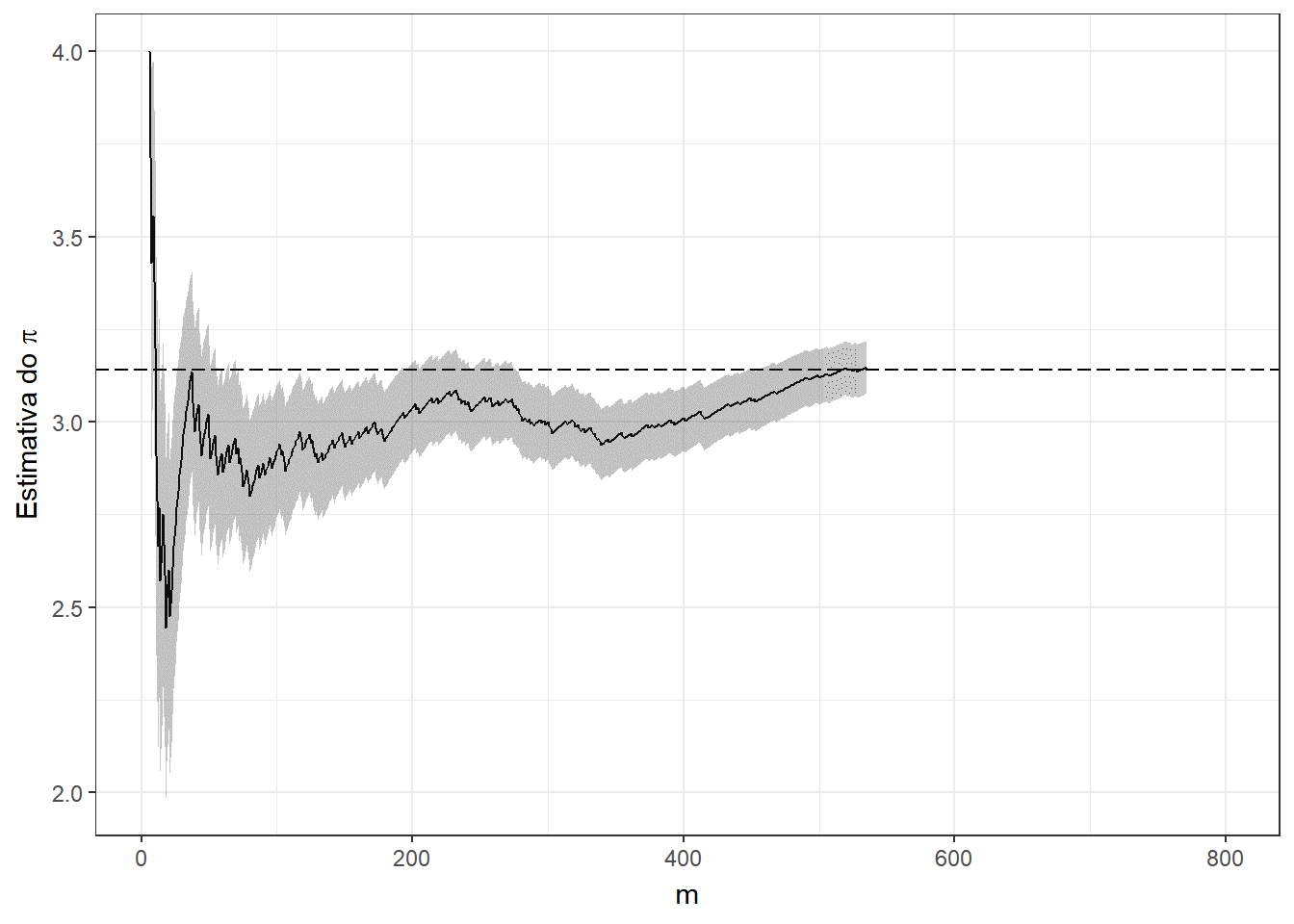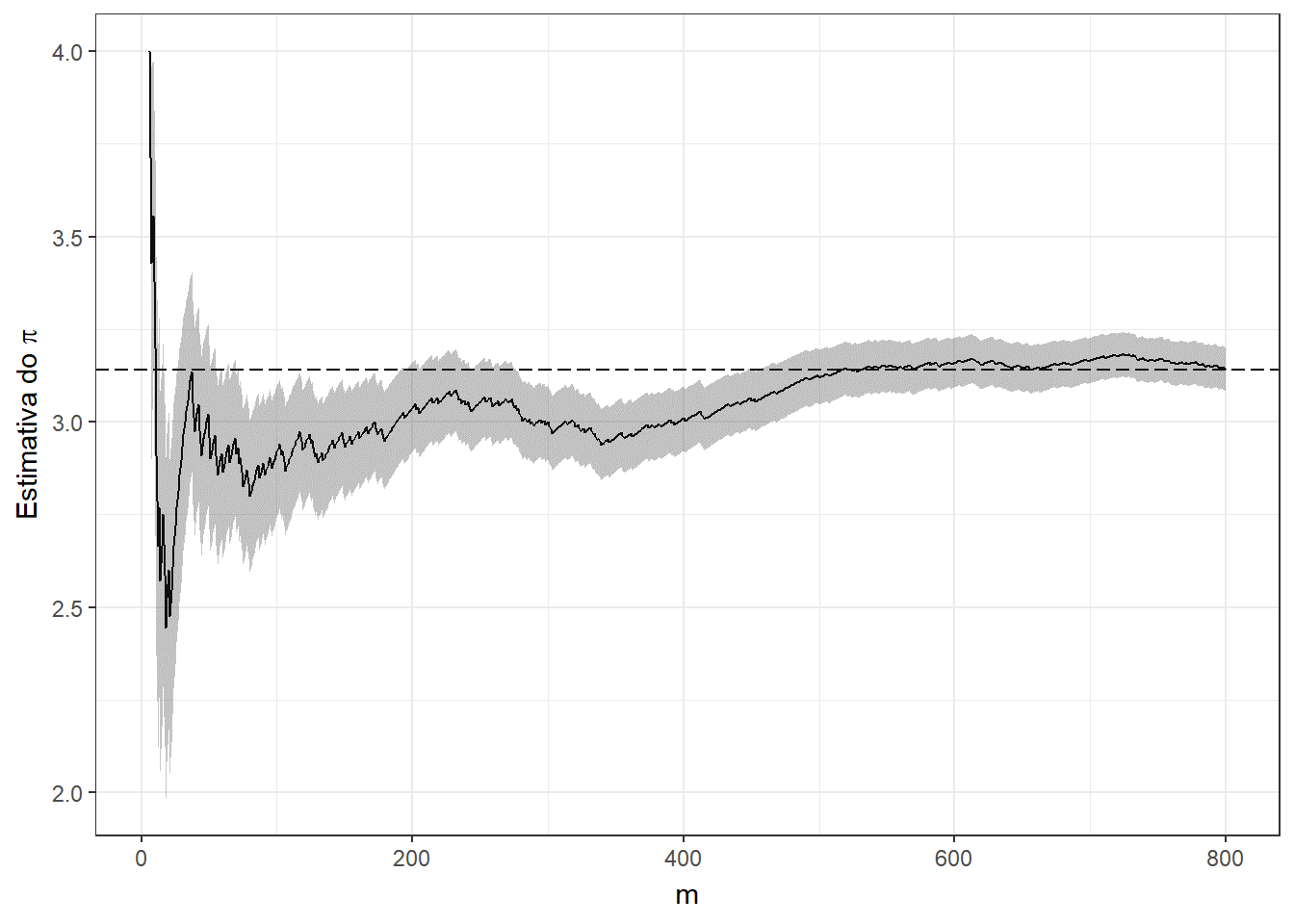
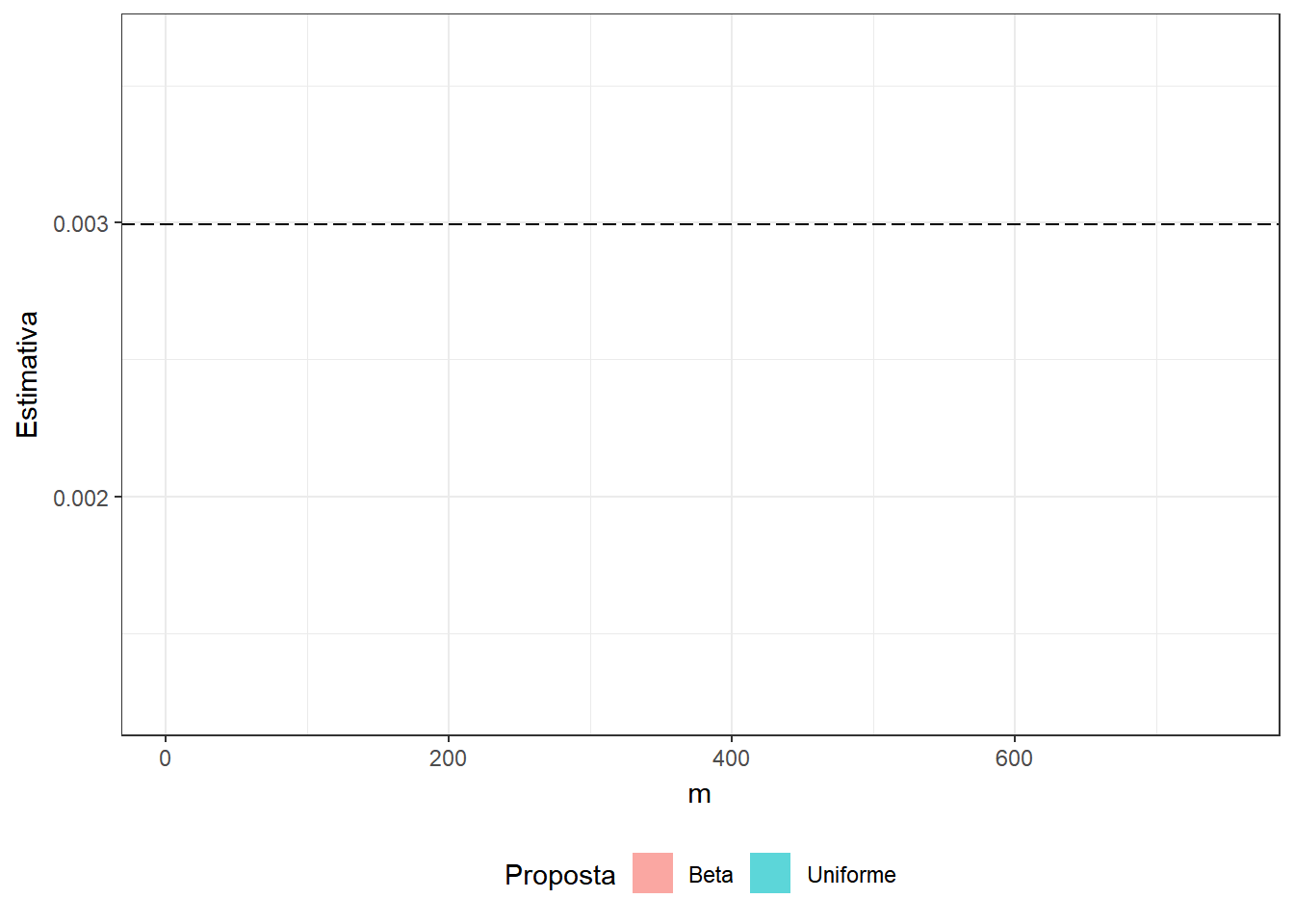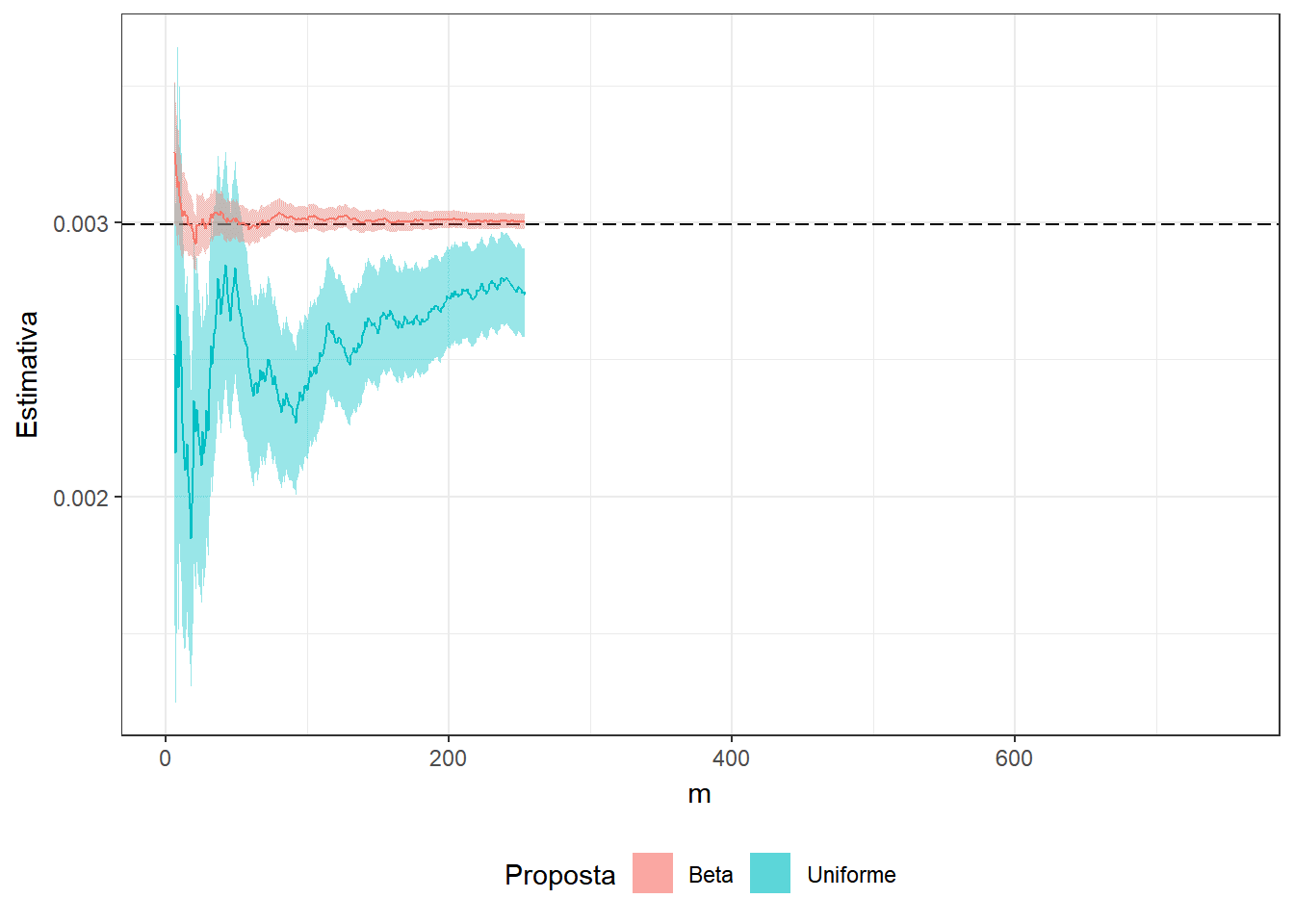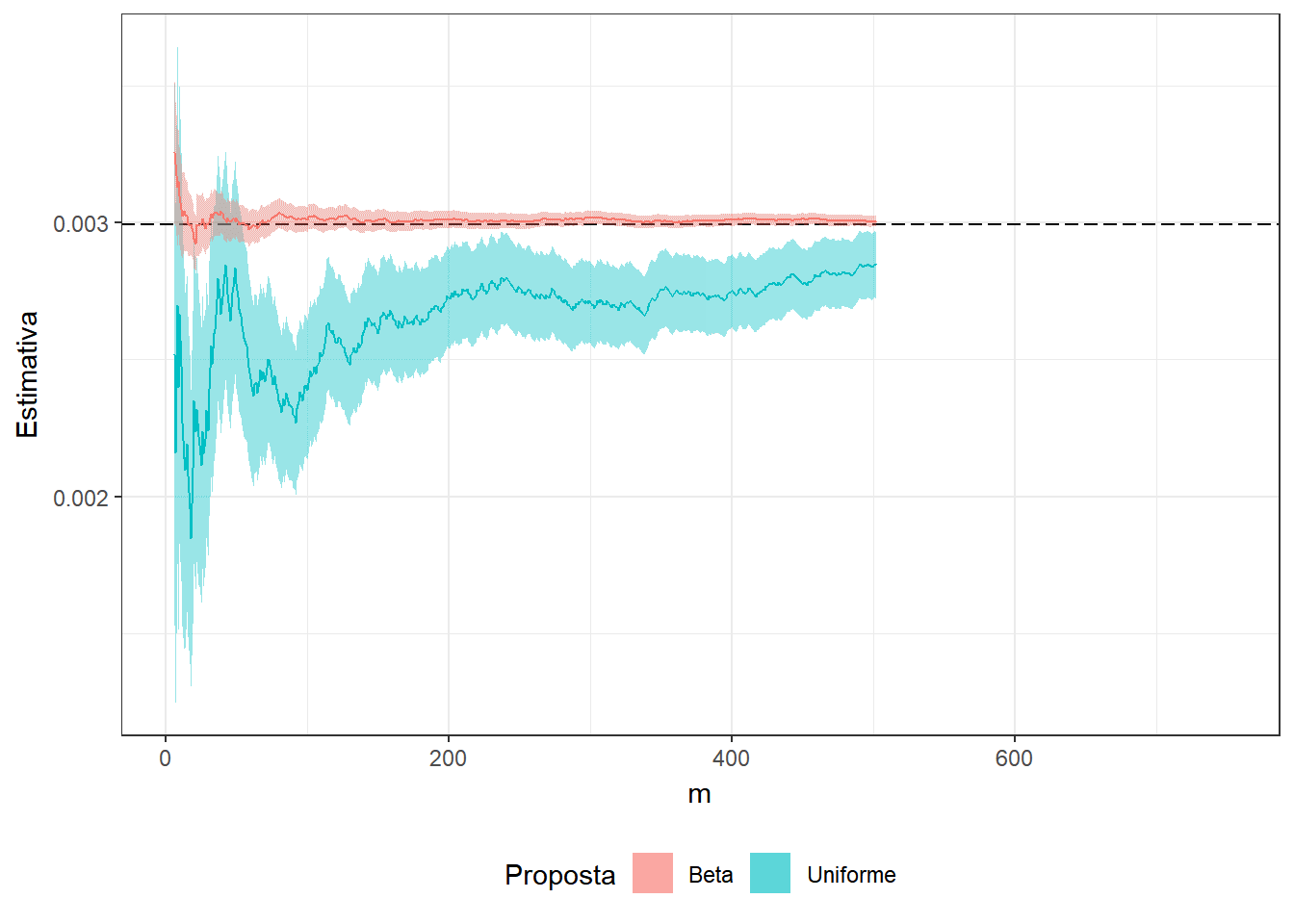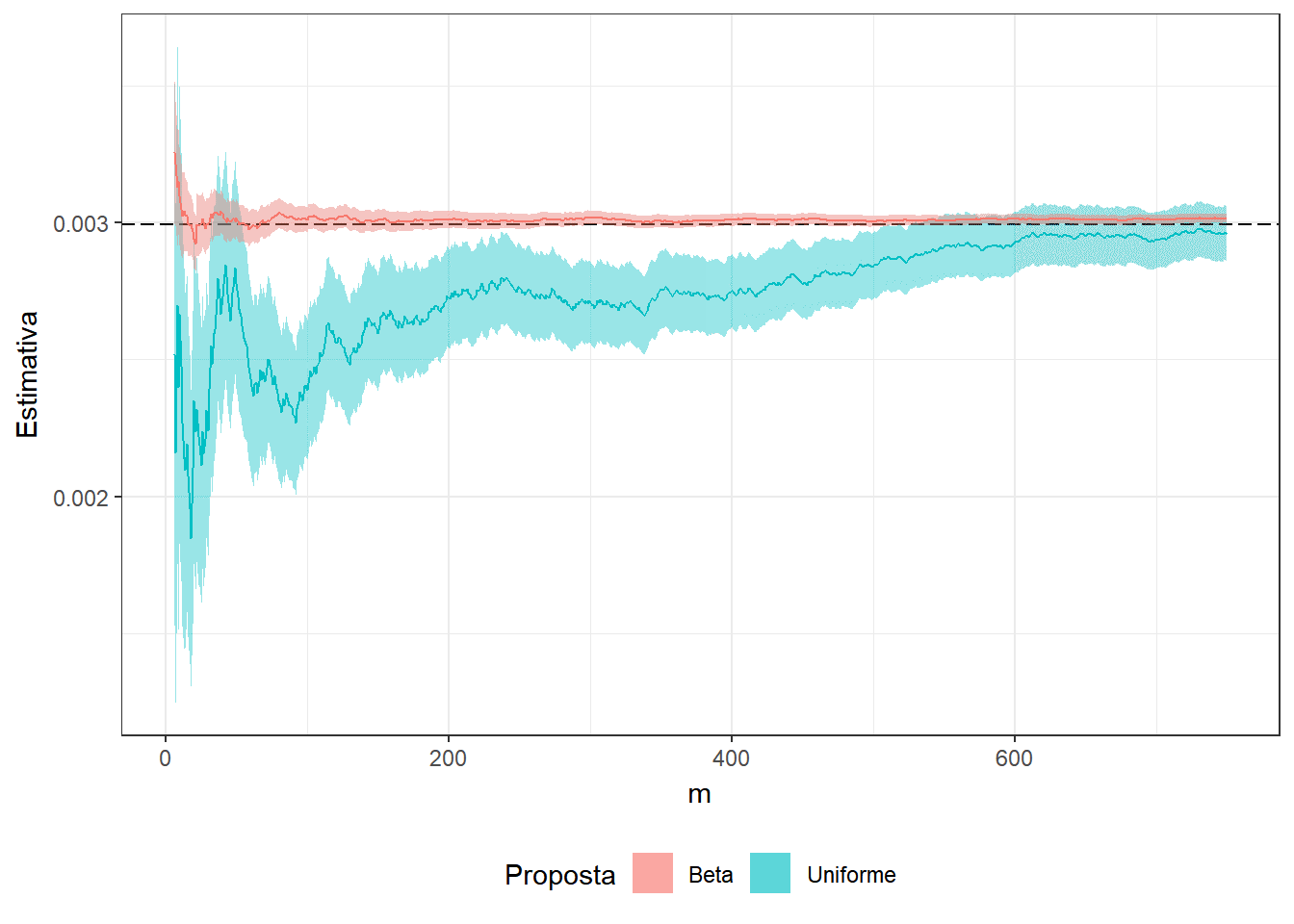
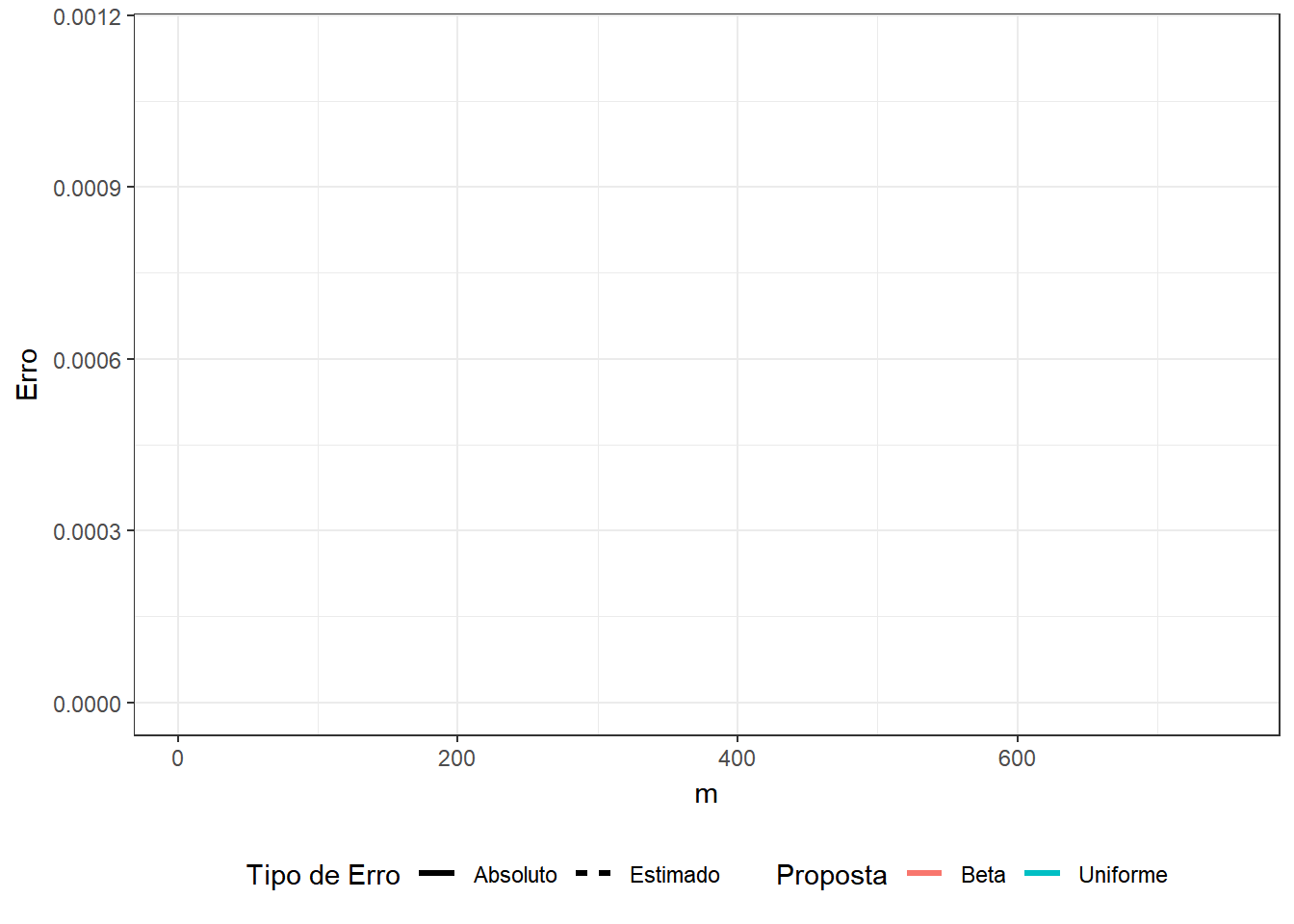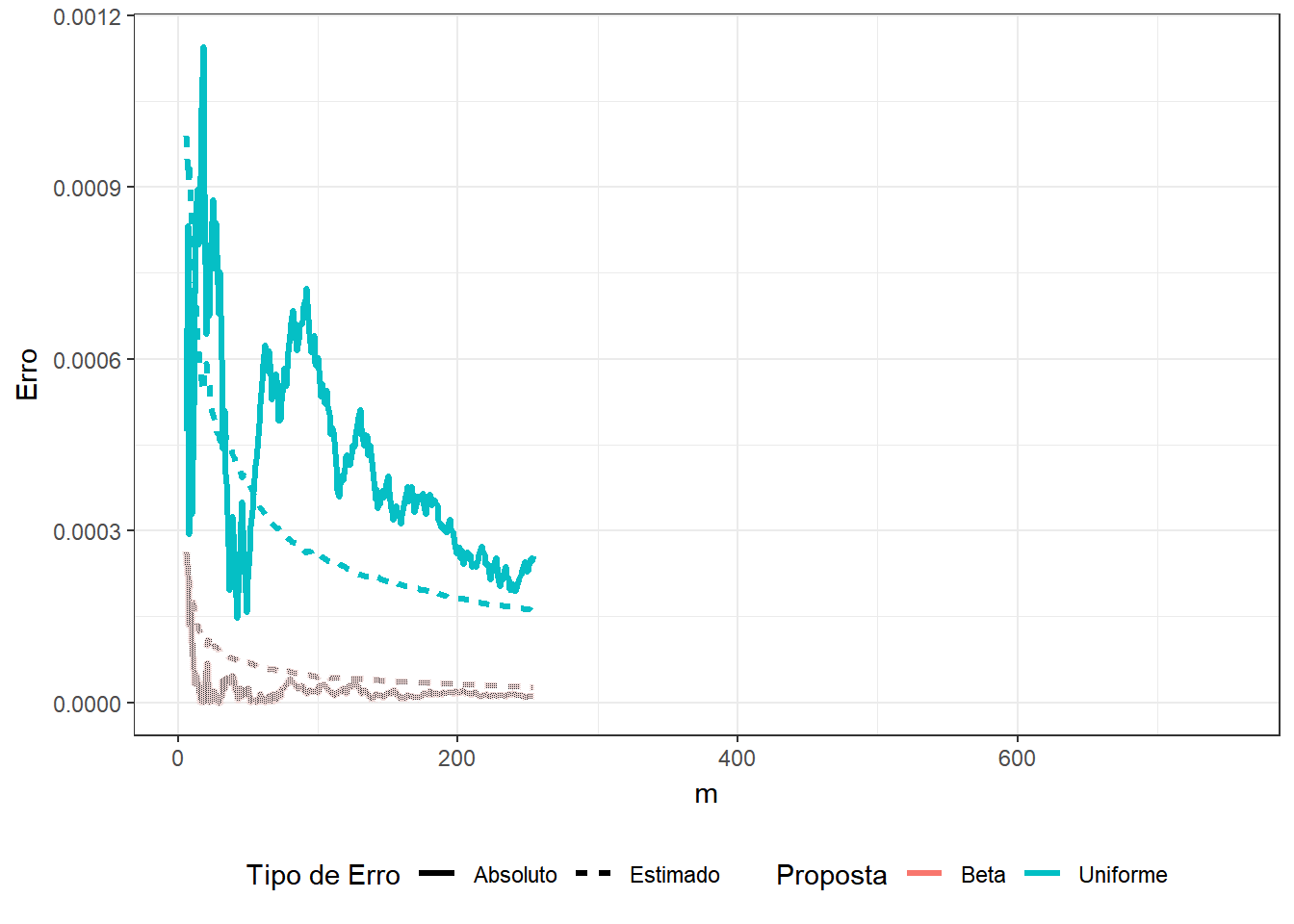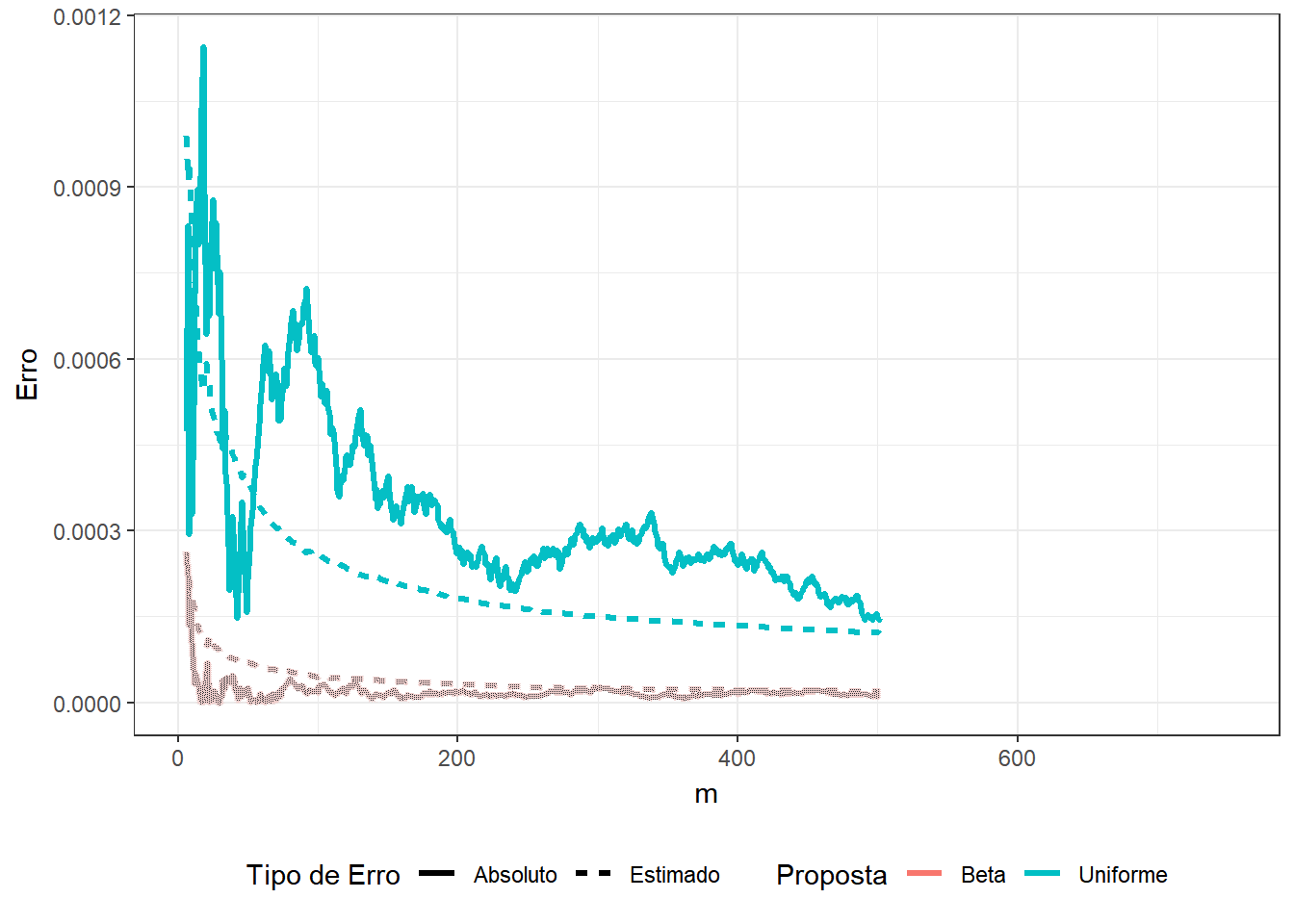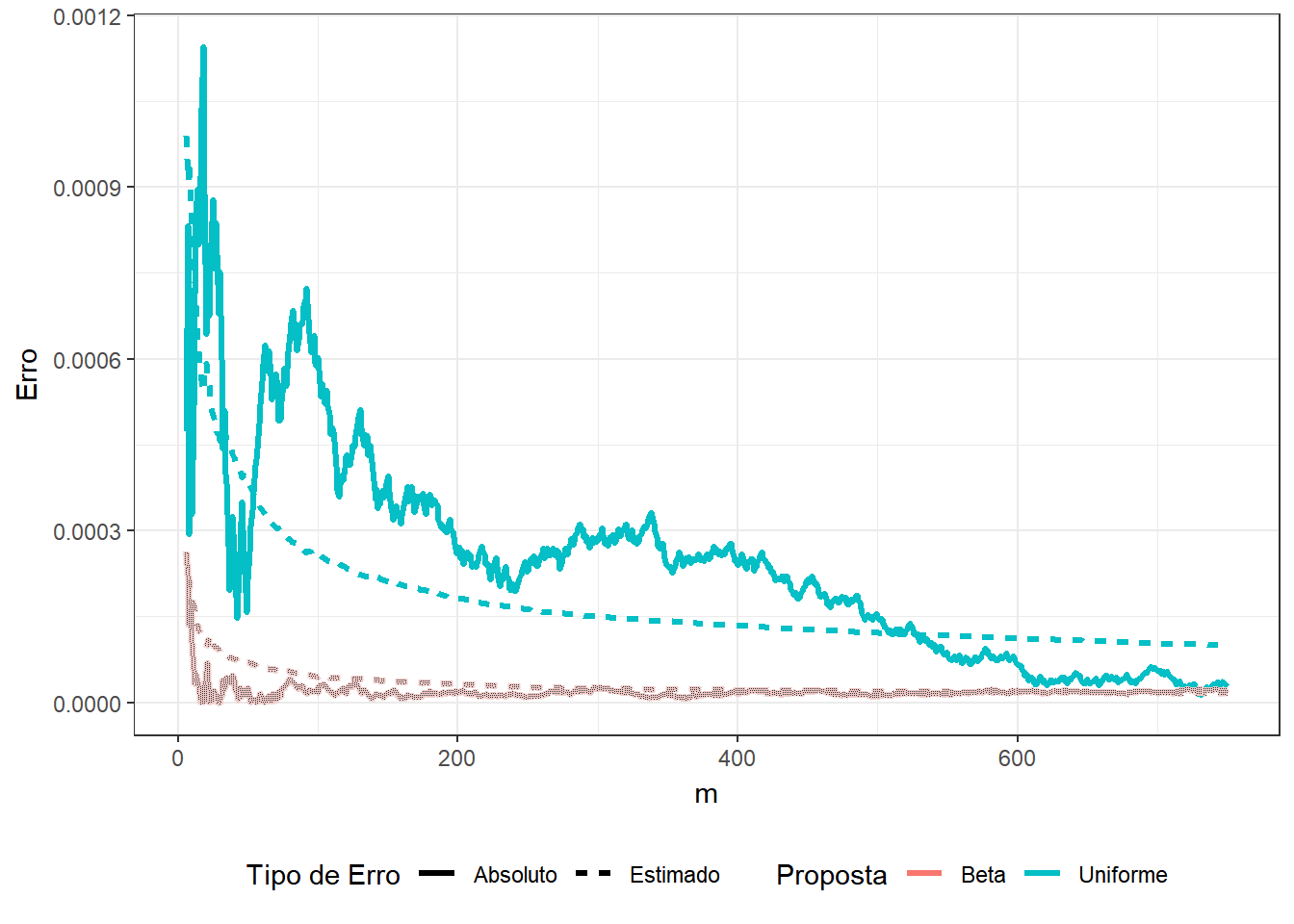
Exemplo 2. Suponha que você não sabe que \[\displaystyle \int_0^1 x^3(1-x)^5e^xdx = 74046 - 27240e\approx0.0029928\] e deseja estimar o resultado usando o método de Monte Carlo. Assim, considere as duas propostas a seguir
1. \(U \sim Unif (0,1)\) e a integral pode ser escrita como \(E\left[U^3(1-U)^5e^U\right]\);
2. \(Y \sim Beta(4,6)\) de modo que
\(\displaystyle \int_0^1 y^3(1-y)^5e^y dy\) \(=\beta(4,6)\displaystyle \int_0^1 e^y~~\frac{y^{4-1}(1-y)^{6-1}}{\beta(4,6)}~dy\) \(=\beta(4,6)E\left[e^Y\right]\).

\(~\)

Exemplo 3. Região HPD Suponha que \(\boldsymbol \theta=(\mu,\sigma^2) \sim \textit{Normal-Inv.Gama}(m,v,a,b)\) e deseja-se obter estimativas pontuais e por região para \(\boldsymbol \theta\).
\(~\)
Se não houver um simulador da distribuição Normal-Inv.Gamma diretamente, é possível gerar um ponto \(\boldsymbol \theta_i=(\mu_i,\sigma_i)\) tomando \({\sigma}_i^2 \sim \textit{Inv.Gama}(a,b)\) (ou \(\tau_i \sim \textit{Gama}(a,b)\) e fazer \({\sigma}_i^2=1/\tau_i\)) e \(\mu_i \sim \textit{Normal}(m,{\sigma}_i^2/v)\). Nesse exemplo é fácil simular uma amostra da distribuição posterior e é possível obter estimativas pontuais simplesmente obtendo estatística resumo da amostra simulada, como média, moda, mediana, variância e desvio padrão.
\(~\)
Para construir a região HPD, primeiramente note que
\(R=\left\{\boldsymbol{\theta}\in\Theta :~f(\boldsymbol{\theta} | \boldsymbol{x})\geq h)\right\}=\left\{\boldsymbol{\theta}\in\Theta:~f(\boldsymbol x|\boldsymbol{\theta})f(\boldsymbol{\theta})\geq h^*=c\cdot h\right\}\),
de modo que não é necessário conhecer a constante \(c=f(\boldsymbol{x})\) para realizar essa tarefa. Como nesse exemplo a distribuição a posteriori é conhecida e fácil de ser simulada, considere o algorítmo a seguir para estimar a região HPD de probabilidade \(\gamma\).
\(~\)
1. Simular \(\boldsymbol{\theta}_1,...,\boldsymbol{\theta}_m\) de \(f(\boldsymbol{\theta}|\boldsymbol{x})\);
2. Encontrar \(h\) tal que \(\displaystyle \dfrac{1}{m}\sum_{i=1}^m\mathbb{I}_{R}(\boldsymbol{\theta}_i)=\dfrac{1}{m}\sum_{i=1}^m\mathbb{I}(f(\boldsymbol{\theta}_i|\boldsymbol{x})\geq h)\approx \gamma\)
\(~~~\) i. Calcule \(f(\boldsymbol{\theta}_i|\boldsymbol{x})\), \(i=1,\ldots,m\);
\(~~~\) ii. Ordene esses valores e tome \(h\) como o percentil de ordem \(\gamma\);
3. Fazer o gráfico da curva de nível \(f(\boldsymbol{\theta}|\boldsymbol{x})=h\).

set.seed(666)
a=7; b=7; m=0; v=0.5 # parametros da posteriori
M=10000 # No. de simulações
dpost=Vectorize(function(t1,t2){ #densidade posterior
  extraDistr::dinvgamma(t2,a,b)*dnorm(t1,m,sqrt(t2/v))})
# simulações
df = tibble(sigma2=extraDistr::rinvgamma(M,a,b)) %>%  
  mutate(mu=rnorm(M,m,sqrt(sigma2/v)))
#summarytools::dfSummary(df, graph.magnif = 0.75, valid.col = FALSE, na.col = FALSE)
summarytools::dfSummary(df, plain.ascii = FALSE, style = "grid", 
          graph.magnif = 0.75, valid.col = FALSE, na.col = FALSE, 
          varnumbers = FALSE, headings = FALSE, tmp.img.dir = "./tmp")

Variable	Stats / Values	Freqs (% of Valid)	Graph
sigma2 [numeric]	Mean (sd) : 1.2 (0.5) min < med < max: 0.3 < 1.1 < 7.3 IQR (CV) : 0.6 (0.4)	10000 distinct values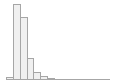
mu [numeric]	Mean (sd) : 0 (1.5) min < med < max: -7.3 < 0 < 6.1 IQR (CV) : 2 (-253.7)	10000 distinct values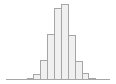

df = df %>% mutate(post=dpost(mu,sigma2))
# variáveis para os gráficos
gama=c(0.99,0.95,0.9,0.8,0.5,0.3,0.1) # prob das regiões
l=quantile(df$post,1-gama)
d=100
x=seq(-4*extraDistr::qinvgamma(0.5,a,b)/v,4*extraDistr::qinvgamma(0.5,a,b)/v,length.out = d)
y=seq(0,extraDistr::qinvgamma(0.996,a,b),length.out = d)
z=matrix(apply(cbind(rep(x,d),rep(y,each=d)),1,function(t){dpost(t[1],t[2])}),ncol=d)
# gráfico da posteriori
plotly::plot_ly(alpha=0.1) %>% 
  plotly::add_surface(x=x, y=y, z=t(z), showscale = FALSE, 
      colorscale=list(c(0,'green'),c(1/4,'yellow'),c(2/4,'orange'),c(3/4,'red'), c(1,'darkred')))

      #colorscale = list(c(0,'#BA52ED'), c(1,'#FCB040')))

# gráfico das regiões HPD de prob. gama=c(0.99,0.95,0.9,0.8,0.5,0.3,0.1)
tibble(x1=rep(x,d),y1=rep(y,each=d),z1=as.vector(z)) %>%
  arrange(z1) %>% mutate(p=1-(cumsum(z1)/sum(z1))) %>% 
  ggplot(aes(x1,y1,z=z1,fill = p)) +
  geom_raster(interpolate = TRUE) +
  jcolors::scale_fill_jcolors_contin("pal3") +
  #scale_fill_distiller(palette = "YlOrRd") +
  geom_contour(breaks=l,col="black") +
  xlab(expression(mu)) + ylab(expression(sigma^2))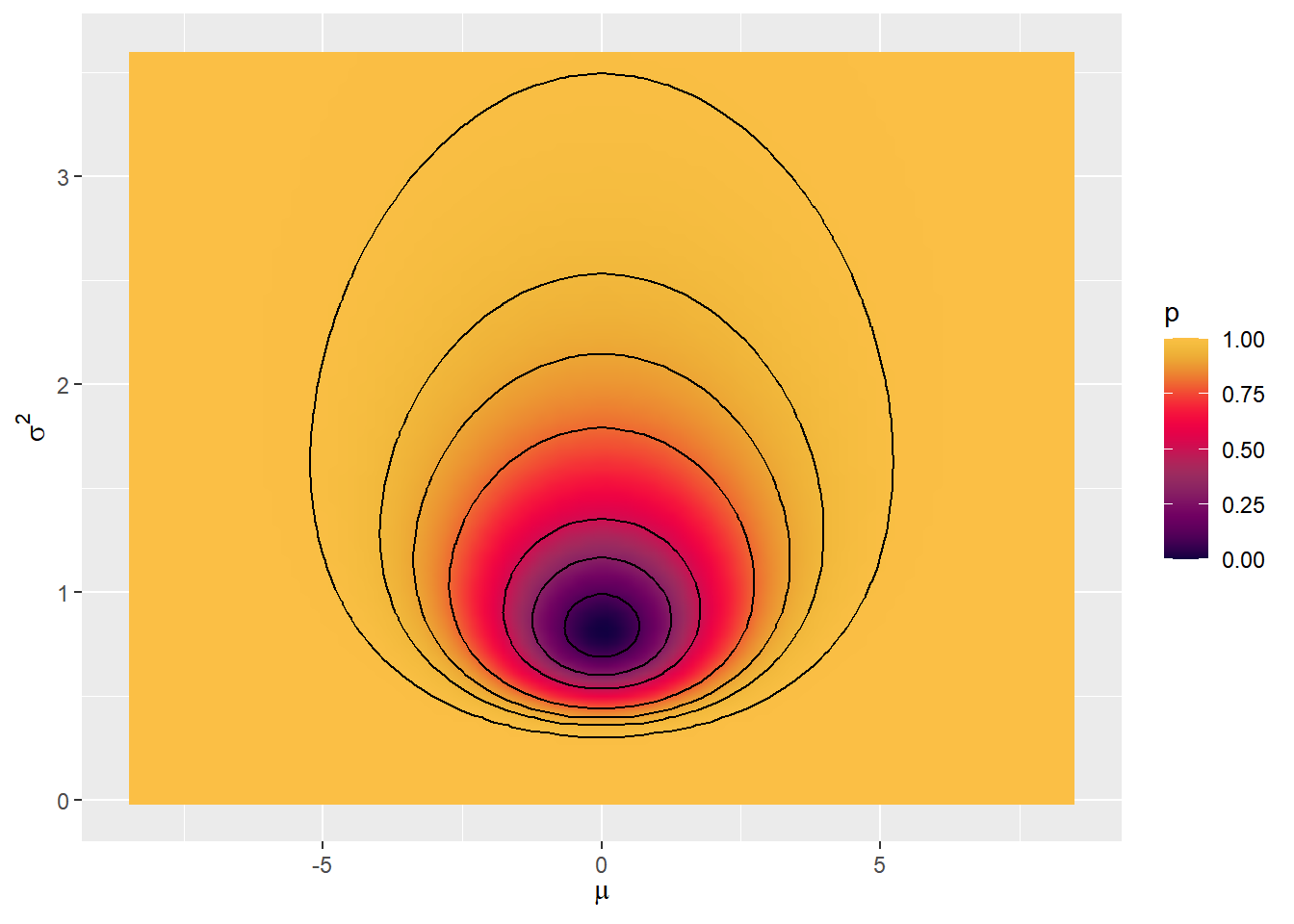

\(~\)

7.2 Monte Carlo com Amostragem de Importância

Considere \(f(\theta|\boldsymbol x)\propto f(\boldsymbol x| \theta)f(\theta)\) e suponha que não se sabe simular observações desta distribuição mas tem-se interesse na quantidade \(E\left[g(\theta)|\boldsymbol x\right]=\displaystyle\int_\Theta g(\theta)f(\theta| \boldsymbol x)d\theta\).

Suponha também que existe uma distribuição \(h(\theta)\) que seja uma aproximação para \(f(\theta|\boldsymbol x)\) (preferencialmente com caudas mais pesadas) da qual sabe-se simular. Então,

\(E\left[g(\theta)| \boldsymbol x\right]\) \(=\displaystyle\int_\Theta g(\theta)f(\theta|\boldsymbol x)d\theta\) \(=\dfrac{\displaystyle \int_\Theta g(\theta)f(\boldsymbol x|\theta)f(\theta)d\theta}{\displaystyle\int_\theta f(\boldsymbol x|\theta)f(\theta)d\theta}\) \(=\dfrac{\displaystyle \int g(\theta)\left(\frac{f(\boldsymbol x|\theta)f(\theta)}{h(\theta)}\right)h(\theta)d\theta}{\displaystyle\int\left(\frac{f(\boldsymbol x|\theta)f(\theta)}{h(\theta)}\right)h(\theta)d\theta}\) \(=\dfrac{\displaystyle\int g(\theta)w(\theta)h(\theta)d\theta}{\displaystyle\int w(\theta)h(\theta)d\theta}\) \(\approx \displaystyle\sum_{i=1}^m \dfrac{w_i}{\sum_{j=1}^mw_j}~g(\theta_i)\),

onde \(w_i=w(\theta_i)=\dfrac{f(\boldsymbol x|\theta_i)f(\theta_i)}{h(\theta_i)}\).

\(~\)

7.3 Método de Rejeição

Considere novamente que o objetivo é simular observações de \(f(\theta|\boldsymbol x)\) mas não é possível fazer isso diretamente. Por outro lado, sabe-se simular dados de uma “distribuição candidata,” \(h(\theta)\), tal que \(f(\theta|\boldsymbol x)\leq Mh(\theta)\), \(\forall \theta \in \Theta\) e para alguma constante \(M\). A ideia do método é rejeitar pontos gerados em regiões em que \(h\) atribui maior probabilidade que \(f\) com probabilidade \(1-\left[f(\theta|\boldsymbol x)~/~Mh(\theta)\right]\). Para que a afirmação anterior faça sentido, \(M\) deve ser tal que \(f(\theta|\boldsymbol x)~/~ Mh(\theta) \leq 1\), \(\forall \theta \in \Theta\), de modo que a melhor escolha para \(M\) é \(M^*=\underset{\Theta}{\sup}\dfrac{f(\theta|\boldsymbol x)}{h(\theta)}\).

r = function(t){dbeta(t,4,2)/dbeta(t,1,1)}
M = optimize(r,c(0,1),maximum = TRUE)
tibble(t = seq(0,1,length.out = 1000)) %>% 
  mutate(f=dbeta(t,4,2), h=dbeta(t,1,1),
         Mh=M$objective*dbeta(t,1,1)) %>% 
  ggplot() + theme_bw() +
  geom_line(aes(x=t,y=f,colour="'Dist. Interesse' f"),lwd=1.1) +
  geom_line(aes(x=t,y=h,colour="'Dist. Candidata' h"),lwd=1.1) +
  geom_line(aes(x=t,y=Mh,colour="M.h"),lwd=1.1) +
  geom_segment(x=0.5,xend=0.5,y=dbeta(0.5,4,2),yend=M$objective*dbeta(0.5,1,1),col="darkgrey") +
  geom_segment(x=0.5,xend=0.5,y=0,yend=dbeta(0.5,4,2)) +
  geom_segment(x=0.25,xend=0.25,y=dbeta(0.25,4,2),yend=M$objective*dbeta(0.25,1,1),col="darkgrey") +
  geom_segment(x=0.25,xend=0.25,y=0,yend=dbeta(0.25,4,2)) +
  geom_segment(x=0.75,xend=0.75,y=dbeta(0.75,4,2),yend=M$objective*dbeta(0.75,1,1),col="darkgrey") +
  geom_segment(x=0.75,xend=0.75,y=0,yend=dbeta(0.75,4,2)) +
  labs(colour="")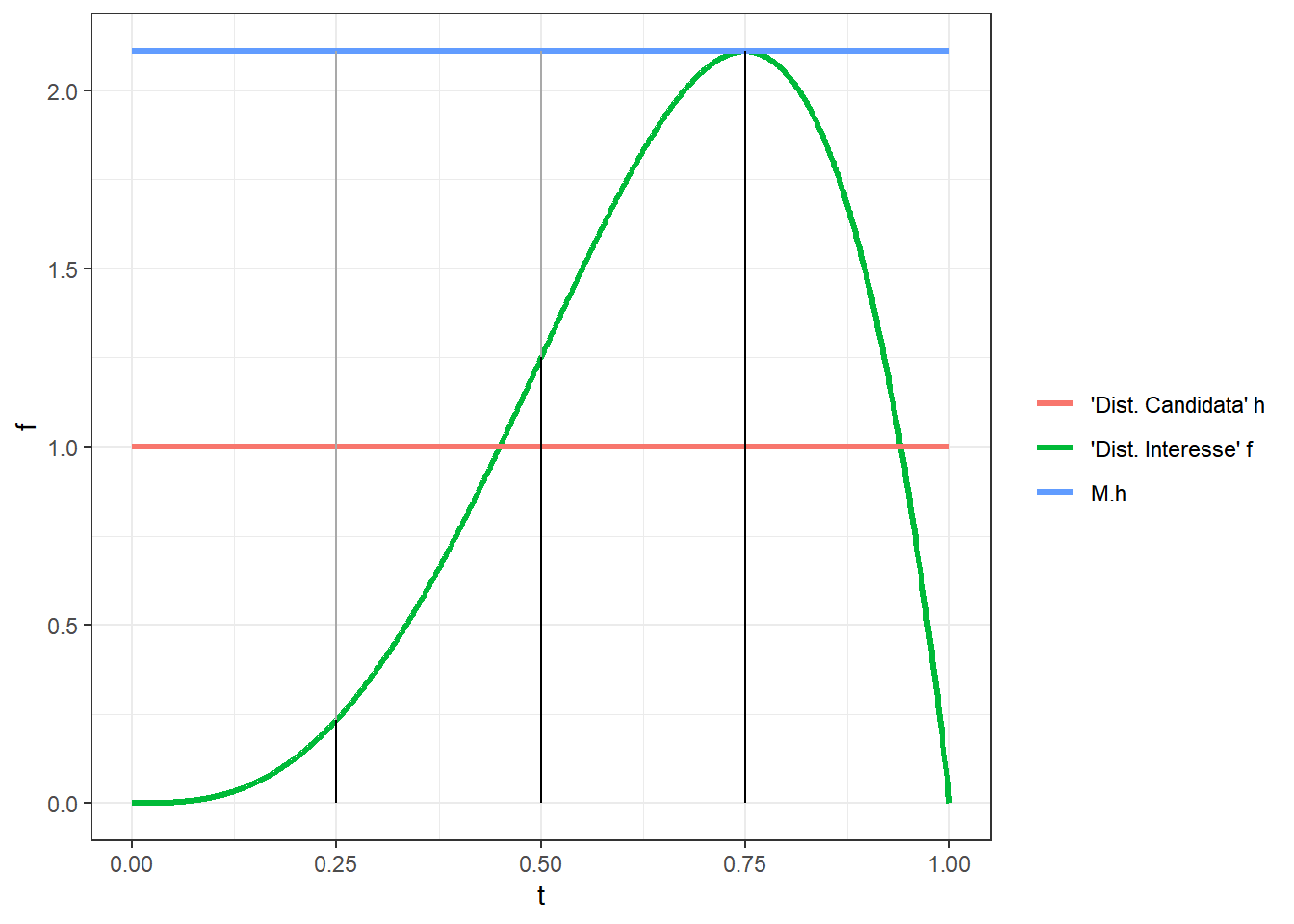

No exemplo apresentado no gráfico acima, suponha que foram gerados os “candidatos” \(0.25\), \(0.5\) e \(0.75\). É possível notar que o ponto \(0.75\) deve ser aceito, o ponto \(0.5\) dever ser aceito com probabilidade \(0.59\) e o ponto \(0.25\) deve ser aceito com probabilidade \(0.11\). A seguir é apresentado o pseudo-algorítmo do método da rejeição.

Para \(i=1,...,m\)
\(~~~\) Repita
\(~~~~~~\) Simule \(u\sim Unif(0,1)\)
\(~~~~~~\) Simule \(\theta^\prime\) da distribuição candidata \(h(\theta)\)
\(~~~\) Até \(u \leq \frac{f(\theta^\prime|\boldsymbol x)}{Mh(\theta^\prime)}\)
\(~~~\) \(\theta_i=\theta^\prime\)
Fim_Para.

r = function(t){(0.4*dnorm(t,-1,1/2)+0.6*dt(t,5,1))/dt(t,1)}
M = optimize(r,c(-8,10),maximum = TRUE)
tibble(t = seq(-5,6,length.out = 1000)) %>% 
  mutate(f=(0.4*dnorm(t,-1,1/2)+0.6*dt(t,5,1)), h=dt(t,1),
         Mh=M$objective*dt(t,1)) %>% 
  ggplot() + theme_bw() +
  geom_line(aes(x=t,y=f,colour="'Dist. Interesse' f"),lwd=1.1) +
  geom_line(aes(x=t,y=h,colour="'Dist. Candidata' h"),lwd=1.1) +
  geom_line(aes(x=t,y=Mh,colour="M.h"),lwd=1.1) +
  geom_vline(xintercept=M$maximum,linetype="longdash",col="darkgrey") +
  labs(colour="")

A linha tracejada representa o ponto na escolha ótima para \(M\). Nesse exemplo é possível notar que na região central, onde é mais “provável” gerar observações de \(h\), a razão \(f(\theta|\boldsymbol x)~/~Mh(\theta)\) é menor que \(0.25\), de modo que há uma grande probabilidade de rejeição. Isso justifica a escolha de distribuições candidatas com caudas pesadas. No caso geral, a probabilidade de aceitação do método é

\(P\left(\left\{(U,\theta) : U \leq \dfrac{f(\theta|\boldsymbol x)}{Mh(\theta)}\right\}\right)\) \(=E_{U,\theta}\left[\mathbb{I}\left(U \leq \dfrac{f(\theta|\boldsymbol x)}{Mh(\theta)}\right)\right]\) \(=E_{\theta}\left[{E_{U|\theta}\left[\mathbb{I}\left(U \leq \dfrac{f(\theta|\boldsymbol x)}{Mh(\theta)}\right)\right]}\right]\) \(=E_{\theta}\left[P\left(U \leq \dfrac{f(\theta|\boldsymbol x)}{Mh(\theta)}~\Big|~\theta\right)\right]\) \(=E_\theta\left[\dfrac{f(\theta|\boldsymbol x)}{Mh(\theta)}\right]\) \(=\displaystyle\int_\Theta\dfrac{f(\theta|\boldsymbol x)}{Mh(\theta)}h(\theta)d\theta\) \(=\dfrac{1}{M}\displaystyle\int_\Theta f(\theta|\boldsymbol x)d\theta=\dfrac{1}{M}\).

\(~\)

No exemplo, a probabilidade de aceitação é \(1/2.434 = 0.41\), ou seja, mais de metade das observações geradas seriam descartadas.

\(~\)

7.4 ABC (Aproximated Bayesian Computation)

O método ABC é uma forma bastante simples de gerar pontos da distribuição a posteriori. Para sua utilização é suficiente saber gerar pontos da distribuição dos dados e da priori, de modo que a verossimilhança nem precisa ser analiticamente conhecida, fato esse que faz com que o método seja dito ser “likelihood-free.”

Suponha o caso em que \(\boldsymbol X\) é discreto com função de verossimilhança \(f(\boldsymbol x|\theta)\), a priori é \(f(\theta)\) e foi observado \(\boldsymbol X=\boldsymbol x_o\). Abaixo é apresentado o pseudo-algorítmo para simular observaçoes da posteriori \(f(\theta |\boldsymbol x_o)\) usando o método ABC.

Algorítmo ABC (\(\boldsymbol X\) discreto)
\(~\)
Para \(i=1,...,m\)
\(~~~\) Repita
\(~~~~~~\) Gere \(\theta^\prime\) de \(f(\theta)\) (priori)
\(~~~~~~\) Gere \(\boldsymbol y = (y_1,...,y_n)\) de \(f(\boldsymbol x|\theta^\prime)\) (verossimilhança)
\(~~~\) Até \(\boldsymbol y =\boldsymbol x_o\)
\(~~~\) \(\theta_i = \theta^\prime\)
Fim_Para

Para verificar que o método funciona no caso discreto, basta ver que

\(f(\theta_i)\) \(=\displaystyle \sum_{y\in \mathfrak{X}}f(\theta_i)f(\boldsymbol y|\theta_i)\mathbb{I}(\boldsymbol y = \boldsymbol x_o)\) \(=f(\theta_i)f(\boldsymbol x_o|\theta_i)\) \(\propto f(\theta |\boldsymbol x_o)\).

\(~\)

No caso em que \(\boldsymbol X\) é contínuo, a probabilidade de gerar uma nova amostra \(\boldsymbol Y\) exatamente igual ao ponto observado \(\boldsymbol x_o\) é zero, \(P(\boldsymbol Y=\boldsymbol x_o)=0\). Nesse caso, o algorítmo é adaptado de modo que são aceitos pontos gerados com \(\Delta\left(\eta(\boldsymbol y),\eta(\boldsymbol x_o)\right) \leq \varepsilon\), onde \(\Delta\) é uma medida de distância conveniente, \(\eta\) é uma estatística (que pode não ser suficiente para \(\theta\)) e \(\varepsilon\) é uma constante de tolerância. O pseudo-algorítmo é apresentado a seguir.

Algorítmo ABC (\(\boldsymbol X\) qualquer)
\(~\)
Para \(i=1,...,m\)
\(~~~\) Repita
\(~~~~~~\) Gere \(\theta^\prime\) de \(f(\theta)\)
\(~~~~~~\) Gere \(\boldsymbol y\) de \(f(\boldsymbol x|\theta^\prime)\)
\(~~~\) Até \(\Delta(\eta(\boldsymbol x),\eta(\boldsymbol y))\leq \varepsilon\)
\(~~~\) \(\theta_i=\theta^\prime\)
Fim_Para

\(~\)

7.5 MCMC - Monte Carlo via Cadeias de Markov

7.5.1 Pequena Introdução às Cadeias de Markov

Definição Um processo estocástico (em tempo discreto) é uma sequência de v.a. \(X_0,X_1,X_2,...\) indexada em \(\mathbb{N}\) (os indices podem indicar, por exemplo, tempo ou espaço ou ?). O conjunto \(E\) onde \(X_i\) toma valores é chamado de espaço de estados.

\(~\)

Definição Um processo estocásticos é dito uma Cadeia de Markov (em tempo discreto) se, \(\forall n \geq 1\) e \(\forall A \subseteq E\),

\(P(X_{n+1}\in A|X_{n}=x_{n},...,X_1=x_1,X_0=x_0)\) \(=P(X_{n+1}\in A|X_{n}=x_{n})\)

\(~\)

Exemplo 1. Suponha uma sequência de v.a. \(\left(X_n\right)_{n\geq 1}\) i.i.d. tais que \(p=P(X_1=1)=1-P(X_1=-1)\). Defina \(S_n=\displaystyle \sum_{i=1}^n X_i\) e \(X_0=c\). O processo estocástico \((S_n)_{n\geq 0}\) é uma Cadeia de Markov. De fato,
\(P\left(S_n=s_n|S_{n-1}=s_{n-1},\ldots,S_0=s_0\right)\) \(=\displaystyle P\left(X_n+S_{n-1}=s_{n}|S_{n-1}=s_{n-1},\ldots,S_0=s_0\right)\)
\(=\displaystyle P\left(X_n=s_n-s_{n-1}|S_{n-1}=s_{n-1},\ldots,S_0=s_0\right)\) \(=\displaystyle P\left(X_n=s_n-s_{n-1}|S_{n-1}=s_{n-1}\right)\) \(=\displaystyle P\left(S_n=s_n|S_{n-1}=s_{n-1}\right)\)

\(~\)

Uma Cadeia de Markov é caracterizada pela distribuição do estado inicial \(X_0\) e pelas probabilidades de transição \(Q(x,A)=P(X_n\in A|X_{n-1}=x)\). Se \(Q(x,A)\) não depende de \(n\), dizemos que é homogênea no tempo.

\(~\)

Para cada \(n\), a cadeia pode

Continuar no estado anterior \(x\), ou seja, \(X_{n+1}=x,\) com probabilidade \(r(x),~ 0\leq r<1\), ou
Saltar para um estado \(y\) segundo uma função de densidade de probabilidade \(q(x,y)\), onde \(0<\displaystyle\int_E q(x,y)dy=1-r(x)\leq 1\) (sub-probabilidade). No caso discreto vamos considerar \(q(x,x)=0\).

Assim, \(Q(x,A)\) \(=P(X_{n+1}\in A|X_{n}=x)\) \(=\displaystyle\int_A q(x,y)dy+r(x)\mathbb{I}_A(x)\).

\(~\)

Suponha que para um dado \(n\), \(X_n\) tem densidade \(\lambda\), isto é, \(P(X_n\in A)=\displaystyle\int_A\lambda(x)dx\). Então, a densidade de \(X_{n+1}\) pode ser obtida por

\(P(X_{n+1}\in A)~\overset{\begin{array}{c} \text{regra da }\\ \text{prob. total}\end{array}}{=}~ \displaystyle\int_E \lambda(x)~Q(x,A)dx\) \(=\displaystyle\int_E\lambda(x)\left[\int_A q(x,y)dy+r(x)\mathbb{I}_A(x)\right]dx\) \(=\displaystyle\int_A\int_E\lambda(x)q(x,y)dxdy+\int_E\lambda(x)r(x)\mathbb{I}_A(x)dx\) \(=\displaystyle\int_A\int_E\lambda(x)q(x,y)dxdy+\int_A\lambda(y)r(y)dy\) \(=\displaystyle \int_A\underbrace{\left[\int_E\lambda(x)q(x,y)dx+\lambda(y)r(y)\right]}_{\text{f.d.p. de }X_{n+1}}dy\).

Assim, a f.d.p de \(X_{n+1}\) é \(\lambda Q(y)= \displaystyle\int_E\lambda(x)q(x,y)dx+\lambda(y)r(y)\)

\(~\)

Dizemos que a densidade \(\pi\) é invariante (estacionária) se as densidades de \(X_{n}\) e \(X_{n+1}\) são iguais (q.c), isto é, \(\pi=\pi Q\) ou \(\int_A \pi(x)dx=\int_E \pi(x)Q(x,A)dx\).

\(~\)

Resultado 1. A afirmação anterior é equivalente a \(\int\pi(x)q(x,y)dx=(1-r(x))\pi(y)\).

\(~\)

Resultado 2. Se a função \(q(x,y)\) satisfaz a condição de reversibilidade, isto é, \(\pi(x)q(x,y)=\pi(y)q(y,x)\), então \(\pi\) é uma medida invariante da cadeia com função de transição \(Q(x,\cdot)\).

\(~\)

Demo 1.
\(\displaystyle\int_E\pi(x)q(x,y)dx\) \(=\displaystyle\int_E\pi(y)q(y,x)dx\) \(=\displaystyle\pi(y)\underbrace{\int_Eq(y,x)dx}_{1-r(y)}\)

\(~\)

Demo 2.
\(\displaystyle\int_E \pi(x)Q(x,A)dx\) \(=\displaystyle\int_E\pi(x)\left[\int_Aq(x,y)dy\right]dx+\int_E \pi(x) r(x)\mathbb{I}_A(x)dx\) \(=\displaystyle\int_A\left[\int_E\pi(x)q(x,y)dx\right]dy+\int_A\pi(x)r(x)dx\) \(=\displaystyle\int_A\left[\int_E\pi(y)q(y,x)dx\right]dy+\int_A\pi(y)r(y)dx\) \(=\displaystyle\int_A\pi(y)\left[\int_Eq(y,x)dx\right]dy+\int_A\pi(y)r(y)dy\) \(=\displaystyle\int_A\pi(y)\Big[1-r(y)\Big]dy+\int_A\pi(y)r(y)dy\) \(=\displaystyle\int_A\pi(y)\Big[1-r(y)+r(y)\Big]dy\) \(=\displaystyle\int_A\pi(y)dy\).

\(~\)

7.5.2 O algoritmo de Metrópolis-Hastings

Suponha que deseja-se gerar observações de \(\pi(\theta)\propto f(\boldsymbol x|\theta)f(\theta)\propto f(\theta|\boldsymbol x)\). Defina uma Cadeia de Markov \((Y_n)_{n\geq 1}\) tal que, no instante \(n\), \(Y_n=y\). No instante \(n+1\), um candidato \(z\) é gerado segundo a densidade \(q(y,z)\) e é aceito com probabilidade \(\alpha(y,z)\). Isto é, se \(Y_n=y\),

\(Y_{n+1}=\left\{\begin{array}{rcl} z,& \text{com probabilidade}& \alpha(y,z)\\ y,& \text{com probabilidade}& 1-\alpha(y,z)\end{array}\right.\),

em que \(\alpha\) é dado por

\(\alpha(y,z)=\left\{\begin{array}{cl} min\left\{ \dfrac{\pi(z)q(z,y)}{\pi(y)q(y,z)}~,~1\right\},& \text{ se }~ \pi(y)q(y,z)>0\\ 1,& \text{c.c.}\end{array}\right.\)

\(~\)

Resultado: O algoritmo de M-H gera uma cadeia reversível com respeito a \(\pi\) e, portanto, tem \(\pi\) como distribuição estacionária.

\(~\)

Demo. Deve-se mostrar que \(\pi(y)\underbrace{q(y,z)\alpha(y,z)}_{p(y,z)}=\pi(z)\underbrace{q(z,y)\alpha(z,y)}_{p(z,y)}~.\)
Suponha \(\pi(z)q(z,y)\geq \pi(y)q(y,z)\) (o caso \(~\leq~\) é análogo)
i) Se \(\pi(z)q(z,y)=0\Rightarrow\pi(y)q(y,z)=0\) e vale a reversibilidade.
ii) \(\pi(z)q(z,y)>0 ~\Rightarrow~ \alpha(y,z)=1\) e \(\alpha(z,y)=\dfrac{\pi(y)q(y,z)}{\pi(z)q(z,y)}\).
Nesse caso, \(\pi(z)q(z,y)\alpha(z,y)=\) \(\pi(z)q(z,y)\dfrac{\pi(y)q(y,z)}{\pi(z)q(z,y)}\) \(=\pi(y)q(y,z)\) \(=\pi(y)q(y,z)\alpha(y,z)\)

\(~\)

7.5.3 Amostrador de Gibbs

Suponha que a \(dim(\Theta)>1\) e deseja-se amostrar \(f(\boldsymbol \theta| \boldsymbol x)\) e suponha que é possível obter amostras das distribuições condicionais completas, isto é, de \(f(\theta_i| \boldsymbol \theta_{-i},\boldsymbol x)\), onde \(\boldsymbol \theta_{-i}=(\theta_1,...,\theta_{i-1},\theta_{i+1},\theta_k)\). Note que \(f(\theta_i| \boldsymbol \theta_{-i},\boldsymbol x)\propto f(\boldsymbol \theta| \boldsymbol x)=f(\boldsymbol x|\boldsymbol \theta)f(\boldsymbol \theta)\). O método do Amostrador de Gibbs é um caso particular do algorítmo de Metrópolis-Hastings em que é gerada uma cadeia \(\left(\boldsymbol \theta^{(n)}\right)_{n\geq 1}\) com \(\alpha(\boldsymbol{y},\boldsymbol{z})=1\) e \(q(\boldsymbol{y},z)=f\left({\theta}_j=\boldsymbol{z}~ \big|~ \boldsymbol{\theta}_{-j}=\boldsymbol{y},~\boldsymbol{x}\right)\), gerada segundo o algorítmo a seguir.

Algorítmo - Amostrador de Gibbs
\(~\)
\(~~~\) Defina uma “chute inicial” \(\boldsymbol \theta^{(0)}\) (por exemplo, gerado da priori \(f(\boldsymbol \theta)\) ou fixado) Para \(i=1,...,m\)
\(~~~\) Gere \(\theta_1^{(i)}\) de \(f(\theta_1| \boldsymbol \theta_{-1}^{(i-1)},\boldsymbol x)\)
\(~~~\) Gere \(\theta_2^{(i)}\) de \(f(\theta_2| \theta_{1}^{(i)}, \theta_{3}^{(i-1)},\ldots, \theta_{k}^{(i-1)} ,\boldsymbol x)\)
\(~~~\) \(~~~\vdots\)
\(~~~\) Gere \(\theta_{k-1}^{(i)}\) de \(f(\theta_{k-1}| \theta_{1}^{(i)},\ldots, \theta_{k-2}^{(i)}, \theta_{k}^{(i-1)} ,\boldsymbol x)\)
\(~~~\) Gere \(\theta_k^{(i)}\) de \(f(\theta_k| \boldsymbol \theta_{-k}^{(i)} ,\boldsymbol x)\)
Fim_Para

\(~\)

Os métodos de Metropolis-Hastings descritos anteriormente geram observações de cadeias de Markov com distribuição estacionária que coincide com a posteriori. Contudo, deve-se tomar dois cuidados para a utilização de métodos de Monte Carlo usando essas observalções. O primeiro é que é necessário verificar se a cadeia já atingiu a estacionariedade. Essa verificação é feita, em geral, observando os gráficos das cadeias geradas e, em geral, as primeiras \(b\) observações são descartadas (burn-in). Outra possibilidade para verificar a estacionariedade da cadeia, bem como a influência do chute inicial, é gerar duas ou mais cadeias iniciando-se de pontos distintos. Outro problema é a dependência entre as observações geradas. Para contornar esse problema, normalmente uma distância \(k\) entre as observações que serão consideradas na amostra final (thin) e as observações entre estas são descartadas. Assim, a amostra final é formada pelos pontos \(\boldsymbol \theta_b, \boldsymbol \theta_{b+k}, \boldsymbol \theta_{b+2k},\ldots,\boldsymbol \theta_{M}\).

\(~\)

Exemplo 1. Seja \(X_1,\ldots,X_n\) c.i.i.d. tais que \(X_i~|~\theta_1,\theta_2 \sim \textit{Exp}\left(\theta_1\theta_2\right)\) e considere que a priori \(\theta_i \sim \textit{Gama}\left(a_1,b_i\right)\), \(i=1,2\). Assim,
\(f(\boldsymbol \theta|\boldsymbol x)\) \(\propto f(\boldsymbol x|\boldsymbol \theta) f(\theta_1)f(\theta_2)\) \(\propto (\theta_1 \theta_2)^n~e^{-\theta_1\theta_2\sum x_i}~~\theta_1^{a_1-1}e^{-b_1\theta_1}~~\theta_2^{a_2-1}e^{-b_2\theta_2}\) \(\propto \theta_1^{a_1+n-1}~\theta_2^{a_2+n-1}~~e^{-b_1\theta_1-b_2\theta_2 -\theta_1\theta_2\sum x_i}~.\)
Essa distribuição não é conhecida mas é possível obter as distribuições condicionais completas
\(f(\theta_i|\theta_j,\boldsymbol x) \propto \theta_i^{a_i+n-1}~e^{-\left[b_i \theta_j\sum x_i\right]\theta_i}\) \(\Longrightarrow \theta_i~|~\theta_j,\boldsymbol x \sim \textit{Gama}\left(a_i+n,b_i+\theta_j\sum x_i\right)\),
e, portanto, é possível simular observações da posteriori usando o amostrador de Gibbs.

set.seed(666)
a1=2; b1=3
a2=3; b2=2
n=8
sumx=4
M=10000
theta1=vector(length = M)
theta2=vector(length = M)
theta1[1] = 4
theta2[1] = 4
for(i in 2:M){
  theta1[i] = rgamma(1,a1+n,b1+theta2[i-1]*sumx)
  theta2[i] = rgamma(1,a2+n,b2+theta1[i]*sumx)
}
m=1000; sel=seq(1,m)
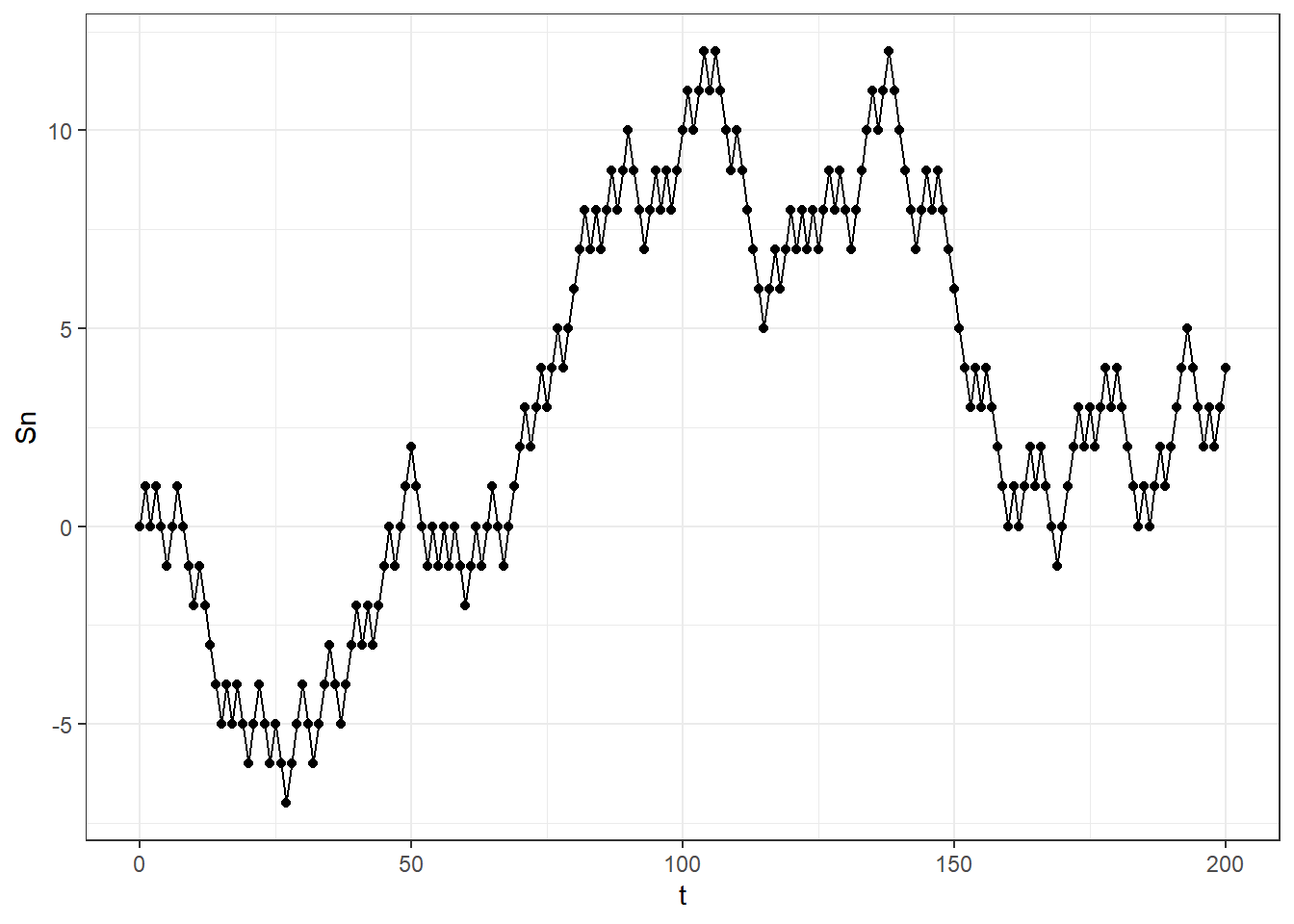
tibble(theta1=theta1[sel],theta2=theta2[sel],t=seq(1,length(sel))) %>%
  ggplot() + theme_bw() +
  geom_path(aes(theta1,theta2),col="darkgrey") +
  geom_point(aes(theta1,theta2)) +
  xlab(expression(theta[1])) + ylab(expression(theta[2])) +
  gganimate::transition_manual(t, cumulative = TRUE)

A seguir, são apresentados os gráficos das cadeias geradas e das autocorrelações.
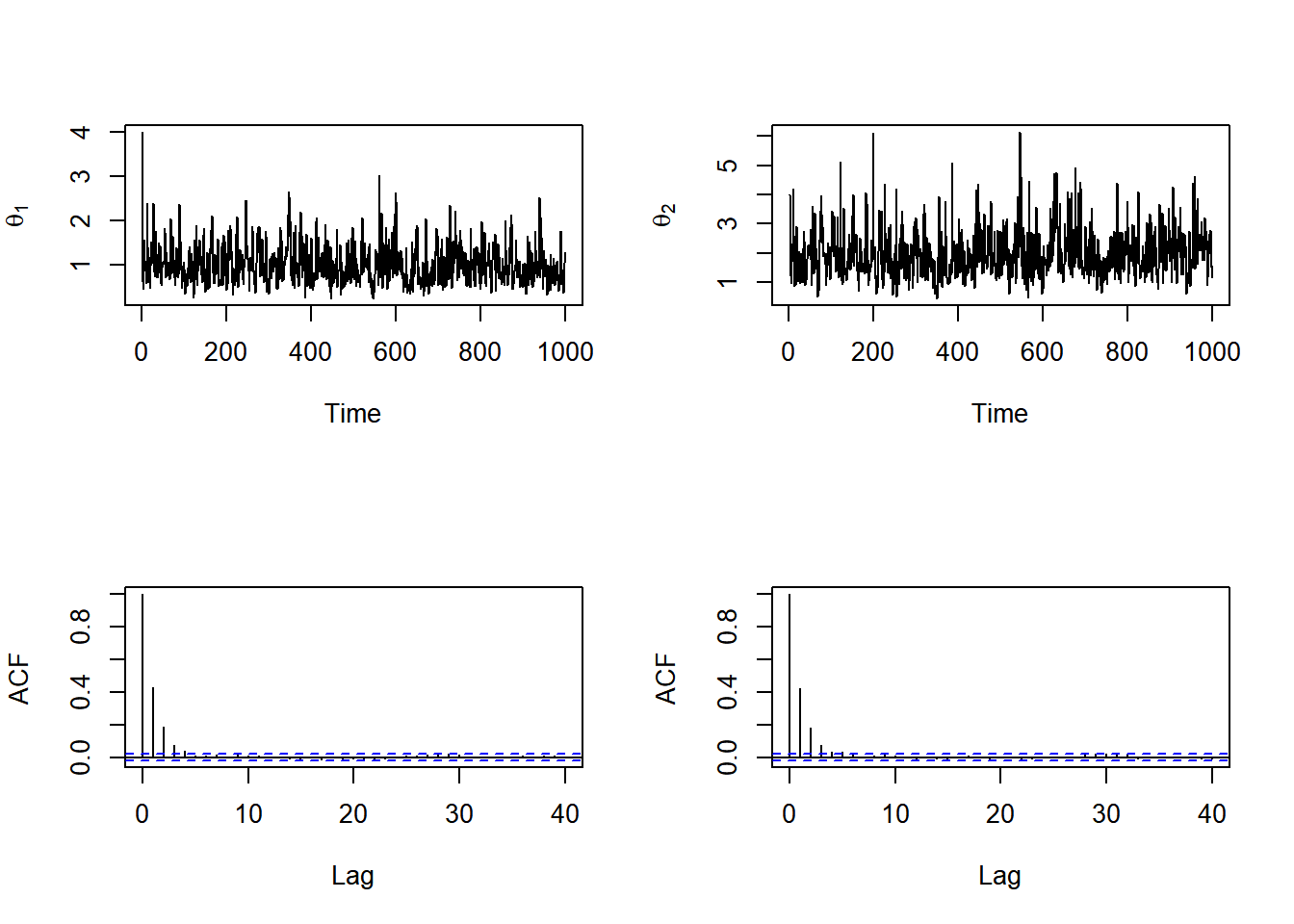Aparentemente, a cadeia converge rapidamente para a distribuição estacionária mas as autocorrelações entre observações consecutivas é alta. Assim, vamos descartar as 10 primeiras observações e considerar saltos de tamanho 5. Os novo gráficos são apresentados abaixo.
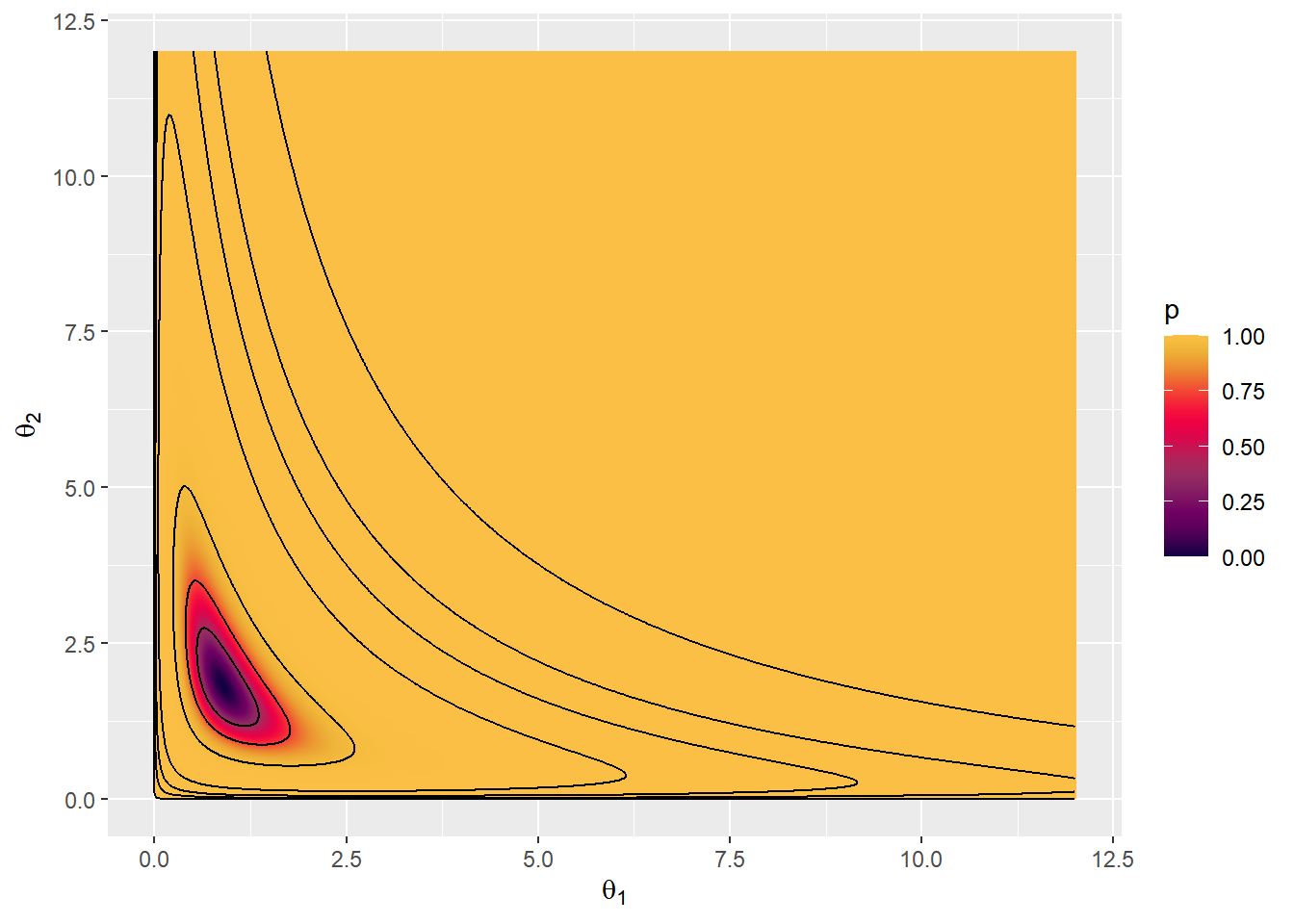
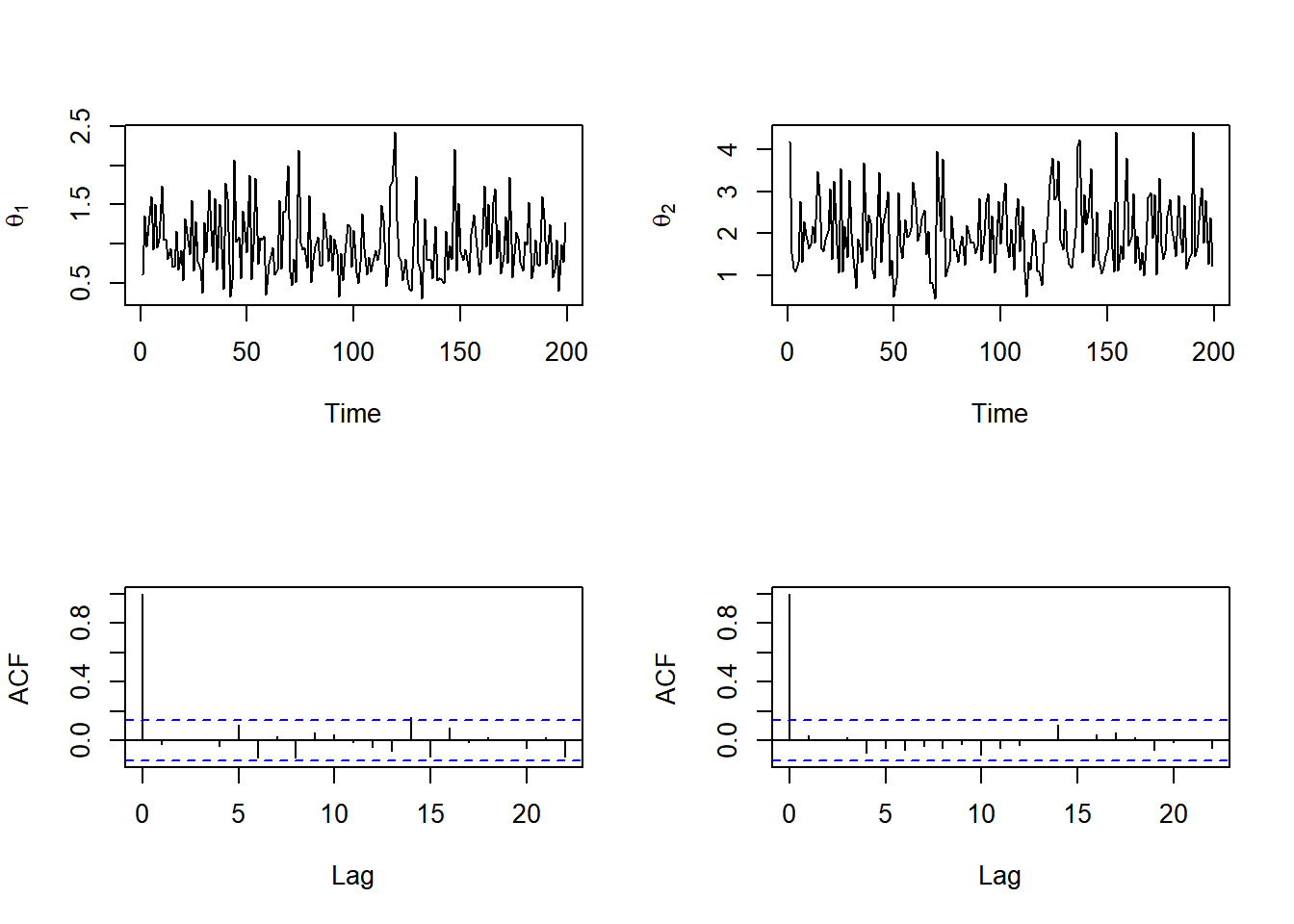Por fim são apresentadas as estimativas das densidades marginais e as regiões HPD.

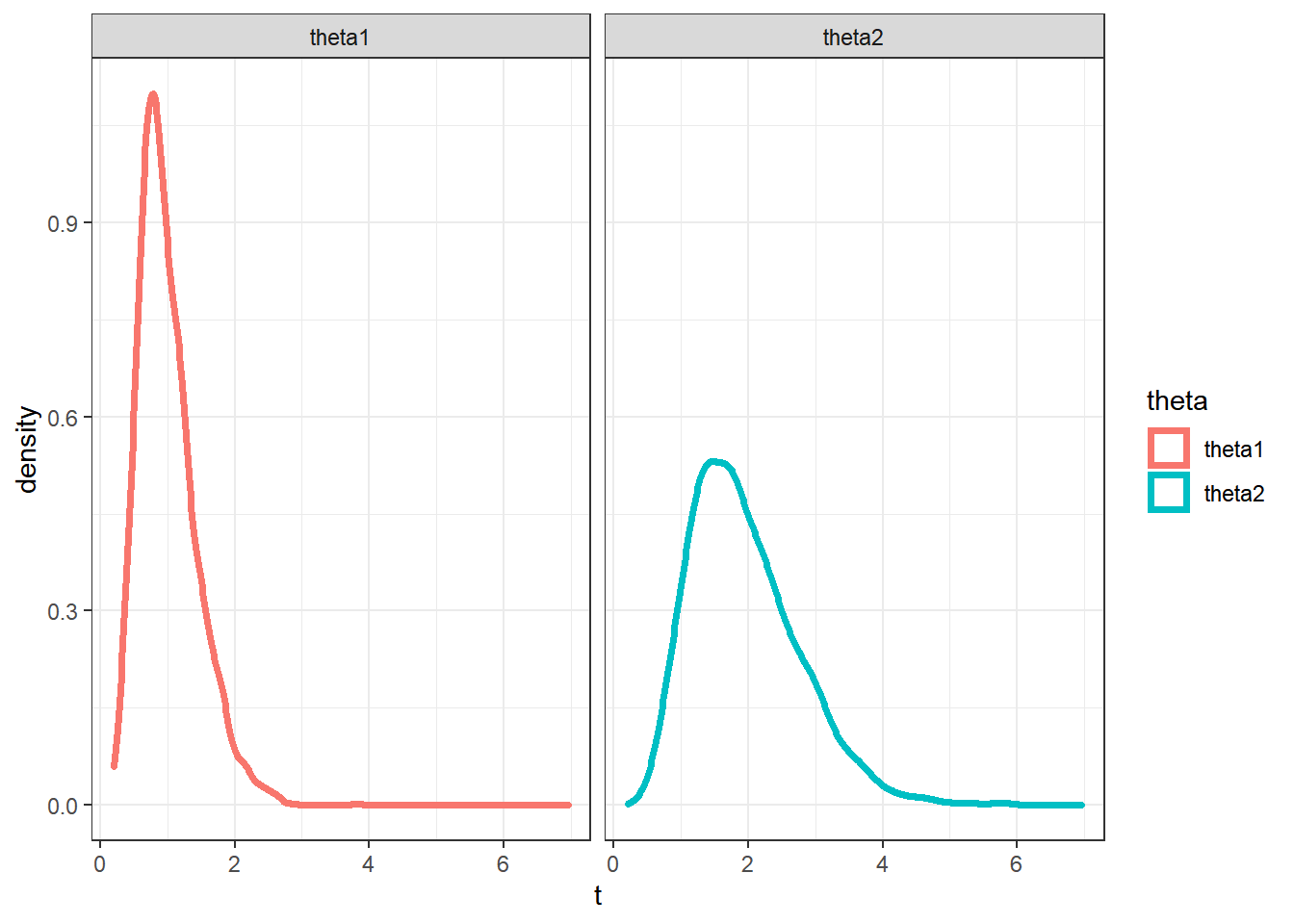
sel=seq(10,M,5)
dpost=Vectorize(function(t1,t2){ #densidade posterior
  exp((n-1)*log(t1*t2)+dexp(sumx,t1*t2,log=TRUE)+dgamma(t1,a1,b1,log=TRUE)+dgamma(t2,a2,b2,log=TRUE))})
# simulações
df = tibble(theta1=theta1[sel],theta2=theta2[sel]) %>% 
      mutate(post=dpost(theta2,theta2))
# variáveis para os gráficos
gama=c(0.99,0.95,0.9,0.8,0.5,0.3,0.1) # prob das regiões
l=quantile(df$post,1-gama)
d=1000
x=seq(0,12,length.out = d)
y=seq(0,12,length.out = d)
z=apply(cbind(rep(x,d),rep(y,each=d)),1,function(t){dpost(t[1],t[2])})
# gráfico das regiões HPD de prob. gama=c(0.99,0.95,0.9,0.8,0.5,0.3,0.1)
tibble(x1=rep(x,d),y1=rep(y,each=d),z1=z) %>%
  arrange(z1) %>% mutate(p=1-(cumsum(z1)/sum(z1))) %>%
  ggplot(aes(x1,y1,z=z1,fill = p)) +
  geom_raster(interpolate = TRUE) +
  jcolors::scale_fill_jcolors_contin("pal3") +
  geom_contour(breaks=l,col="black") +
  xlab(expression(theta[1])) + ylab(expression(theta[2]))