9 Simulação
A simulação computacional é uma ferramenta que permite o estudo de fenômenos complexos, que seriam difíceis ou inviáveis de analisar em contextos reais. Por meio dela, criamos modelos matemáticos que imitam o comportamento de sistemas verdadeiros.
Ou seja, em vez de observar o mundo real diretamente (o que pode ser caro, demorado ou impossível), geramos artificialmente observações que seguem uma determinada distribuição de probabilidade e que se comportam de forma semelhante aos dados reais. Dessa forma, podemos estudar suas propriedades, prever resultados ou testar hipóteses.
9.1 Lei dos Grandes Números
A Lei dos Grandes Números é a base teórica para a simulação ser algo tão confiável. Em termos simples, ela afirma que, à medida que o número de repetições de um experimento aleatório aumenta, a média dos resultados observados tende a se aproximar cada vez mais do valor esperado (média teórica) desse experimento. Ou seja, essa convergência garante que, com um número suficientemente grande de simulações, podemos calcular estimativas precisas para probabilidades e valores médios.
Por exemplo, a Lei dos Grandes Números nos diz que ao lançarmos um dado muitas vezes e calcularmos a média dos resultados, essa média se aproximará de 3,5 (o valor esperado de um dado uniforme discreta de 1 a 6).
De forma semelhante, podemos usar a simulação para observar o que acontece com uma moeda honesta. Se lançarmos 10 vezes, pode dar 7 caras e 3 coroas, mas ao repetir o experimento 10 mil vezes, a proporção de caras de aproxima de 0,5.
set.seed(123)
# Número de lançamentos
n_lancamentos <- 10000
# Simular lançamentos de moeda (0 = coroa, 1 = cara)
resultados <- sample(c(0, 1), size = n_lancamentos, replace = TRUE)
# Calcular a proporção de caras
proporcao_caras <- sum(resultados) / n_lancamentos
cat("Número de lançamentos:", n_lancamentos, "\n")## Número de lançamentos: 10000## Proporção de caras simulada: 0.4983# Para ver a convergência ao longo do tempo (Lei dos Grandes Números)
proporcoes_acumuladas <- cumsum(resultados) / (1:n_lancamentos)
plot(proporcoes_acumuladas, type = "l",
main = "Convergência da Proporção de Caras",
xlab = "Número de Lançamentos",
ylab = "Proporção de Caras",
ylim = c(0, 1))
abline(h = 0.5, col = "deeppink", lty = 2)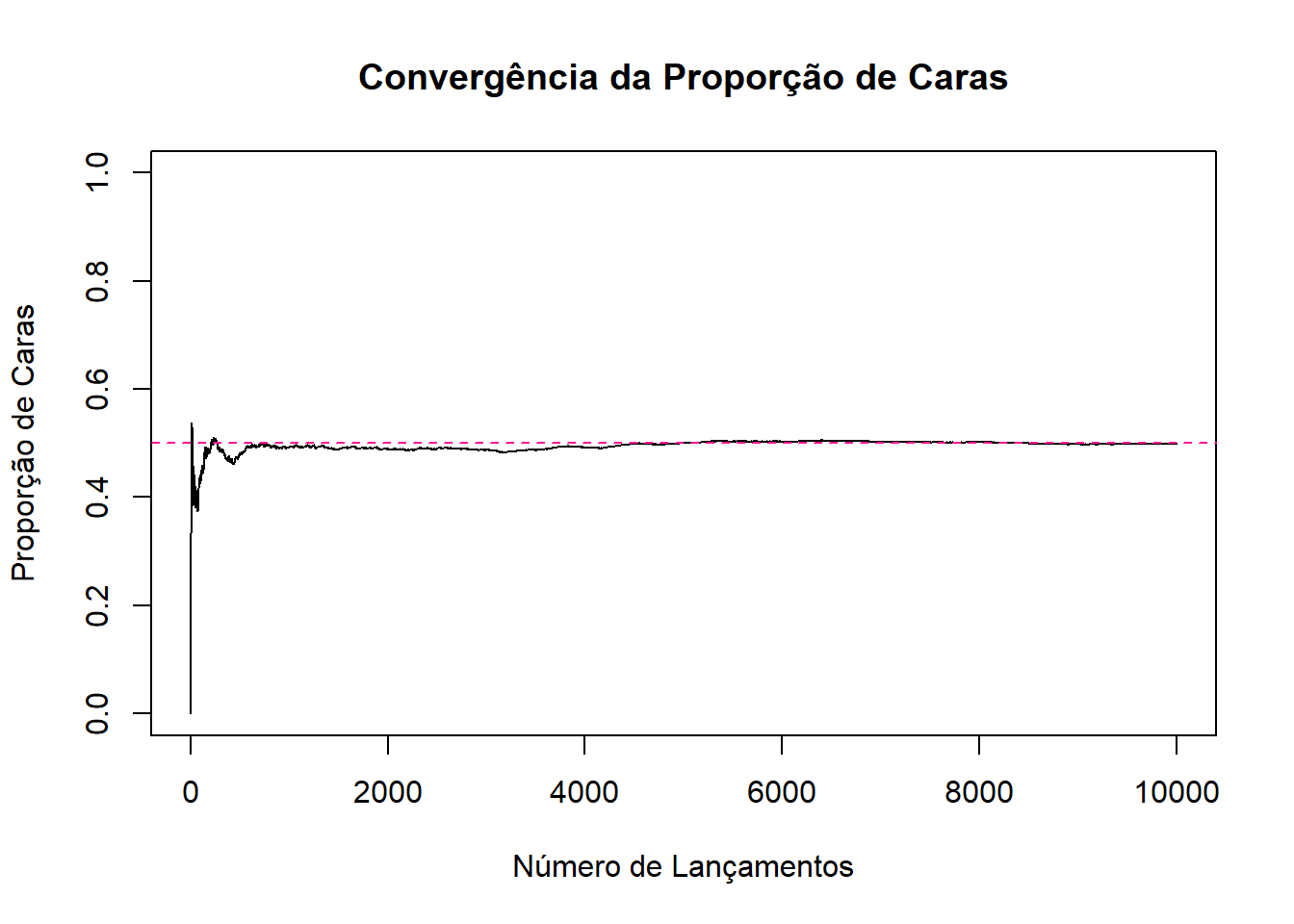
No código acima, primeiro definimos a semente do gerador de números aleatórios set.seed(123), para garantir que os resultados da simulação sejam possíveis de reproduzir, ou seja, toda vez que o código for executado com essa seed, os mesmos números aleatórios serão gerados.
Depois, simulamos os lançamentos da moeda, com 10 mil lançamentos. A função sample() escolhe aleatoriamente entre os valores 0 (coroa) e 1 (cara), com reposição (replace = TRUE). Sendo assim, cada lançamento é independente dos anteriores. O resultados é um vetor com 10 mil resultados de zeros e uns.
Com esses dados, criamos um gráfico da proporção acumulada de caras ao longo dos lançamentos. E por fim, adicionamos uma linha horizontal pontilhada no valor de 0,5 (o valor esperado de caras de uma moeda justa). Dessa forma, conseguimos visualizar como a média de caras observadas se aproximam do valor esperado (0,5).
Observe que no início, com poucos lançamentos, a proporção de caras varia bastante, mas conforme o número de lançamentos aumenta, a linha da proporção acumulada se aproxima cada vez mais de 0,5, confirmando o que a Lei dos Grandes Números nos diz.
9.2 Método de Monte Carlo
O Método de Monte Carlo é uma técnica de simulação, baseada na amostragem aleatória para obter resultados numéricos. Esse método funciona gerando um grande número de amostras aleatórias de uma distribuição de probabilidade e, com isso, estimando uma quantidade de interesse.
Como exemplo, imagine que queremos estimar a área de uma forma irregular. Podemos fazer isso gerando pontos aleatórios dentro de um quadrado que a contém e contar a proporção de pontos que caem dentro da forma irregular.
Utilizando essa ideia, aplicaremos o método de Monte Carlo para estimar a área de um círculo, a ideia é “jogar” pontos aleatoriamente dentro de um quadrado conhecido e ver quantos desses pontos caem dentro do círculo inscrito nesse quadrado.
Pense em um círculo centrado na origem (ponto (0, 0)) e de raio 1. Ou seja, ele ocupa a região: \(x^2 + y^2 \leq 1\). Esse círculo está inteiramente contido dentro de um quadrado que vai de [-1, 1] tanto no eixo \(x\), quanto no eixo \(y\), isto é, o quadrado tem lado 2.
Sabemos que a área real de um círculo é:
\[ \text{Área real} = \pi \cdot r^2 = \pi \cdot 1^2 = \pi \approx 3,1416 \]
Estimando isso pelo metódo de Monte Carlo, vamos gerar aleatoriamente pontos dentro do quadrado e contar quantos desses pontos caem dentro do círculo (satisfazem \(x^2 + y^2 \leq 1\)). A fração de pontos dentro do círculo multiplicada pela área do quadrado (que é 4) nos dá uma estimativa para \(\pi\).
# Define a semente para garantir reprodutibilidade dos resultados
set.seed(123)
# Definir o número de pontos
n_pontos <- 10000
# Gerar coordenadas X e Y aleatórias para os pontos
# dentro do quadrado [-1, 1] x [-1, 1]
x_coords <- runif(n_pontos, min = -1, max = 1)
y_coords <- runif(n_pontos, min = -1, max = 1)
# Calcular a distância ao quadrado até a origem para cada ponto
distancia_ao_quadrado <- x_coords^2 + y_coords^2
# Contar quantos pontos caem dentro do círculo de raio 1
pontos_dentro_circulo <- sum(distancia_ao_quadrado <= 1)
# Calcular a proporção de pontos dentro do círculo
proporcao_no_circulo <- pontos_dentro_circulo / n_pontos
# Estimar a área do círculo (área do quadrado é 4)
area_circulo_estimada <- proporcao_no_circulo * 4
# Mostrar resultados
cat("Total de pontos jogados:", n_pontos, "\n")## Total de pontos jogados: 10000## Pontos que caíram dentro do círculo: 7894## Proporção de pontos dentro do círculo: 0.7894## Estimativa da Área do Círculo (ou Pi): 3.1576## Valor real de Pi (Área do Círculo de raio 1): 3.141593No código acima, geramos dois vetores, com coordenadas x e y uniformemente distribuídas dentro do quadrado que vai de -1 a 1 nos dois eixos. Depois cointamos quantos pontos estão dentro do círculo (a soma dos quadrados das coordenadas seja menor ou igual a 1). E por fim, multiplicamos a proporção de pontos dentro do círculo pela área total do quadrado para obter a estimativa da área do círculo.
Vendo isso de forma visual:
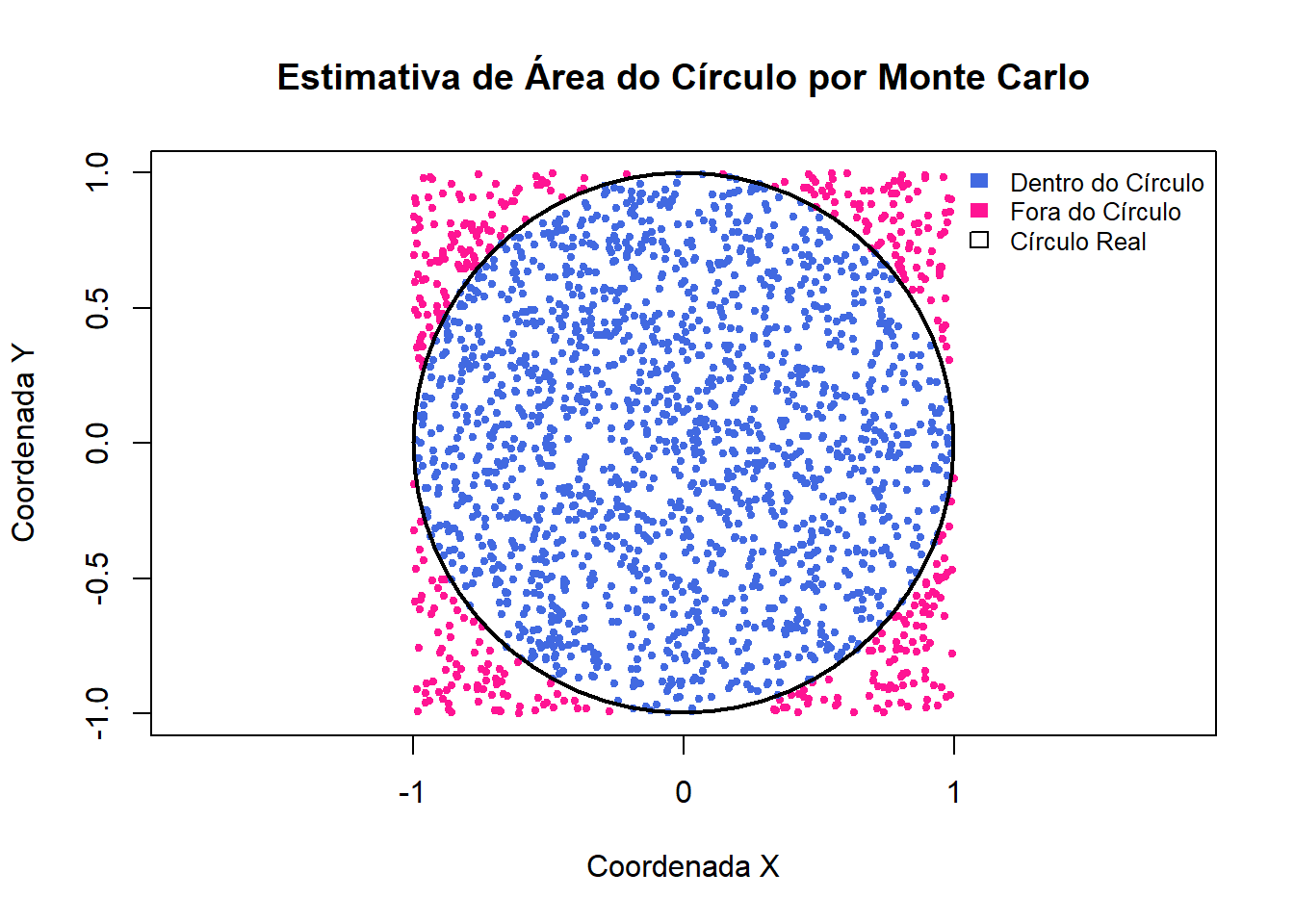
Nesse gráfico, temos o círculo, com os pontos azuis (dentro) e vermelhos (fora), além do contorno do círculo verdadeiro para comparação visual.
9.3 Simulando no R
Vimos como a simulação computacional pode ser usada para estudar fenômenos aleatórios e visualizar resultados teóricos. Agora veremos como simular usando o R.
Primeiro, como já citamos anteriormente, sempre comece as suas simulações com set.seed(), isso garante que, se você ou outra pessoa executar o mesmo código com a mesma semente, os resultados aleatórios serão idênticos, tornando suas simulações reproduzíveis.
9.3.1 Principais funções para simulação no R
O R possui um conjunto de funções para trabalhar com uma determinada distribuição de probabilidade (como a binomial, uniforme, poisson, etc.). Para cada distribuição, existem geralmente quatro funções, prefixadas por letras que indicam sua finalidade.
- r (random): Geração de números aleatórios, a mais utilizada em simulações.
- d (density): função de massa de probabilidade, no caso discreto, ou seja, \(P(X = x)\) e função densidade de probabilidade, no caso contínuo.
- p (probability): Função de distribuição acumulada, ou seja, \(P(X \leq x)\).
- q (quantile): Função quantil, recebe um valor \(p\) e fornece o valor \(q\) que satisfaz \(P(X \leq q) = p\).
Exemplos de funções random:
- rbinom(n, size, prob): distribuição binomial, onde n é o número de simulações (dados gerados), size é a quantidade de ensaios (\(m\) da binomial(\(m, p\))) e p a probabilidade de sucesso de cada ensaio. Note que, para size=1 temos uma distribuição de Bernoulli.
- sample(x, size, replace, prob): amostragem discreta aleatória, onde x é o conjunto de números de onde se quer sortear dados, size é a qunatidade de tentativas, replace é se tem repetição (=TRUE) ou não (=FALSE), ou seja, se tem reposição ou não e prob é um vetor opcional, que corresponde a probabilidade de sucesso de cada elemento do vetor x.
Para distribuições contínuas temos rnorm(), runif(), etc.
Exemplo prático, utilizando a distribuição Binomial
Sabemos que a distribuição binomial modela o número de sucessos em \(n\) tentativas independentes, com probabilidade de sucesso \(p\).
Vamos pegar como exemplo o caso em que jogamos uma moeda honesta 10 vezes e contamos quantas vezes deu cara. Ou seja, temos uma binomial com \(n=10\) e \(p=0,5\). Repetiremos o experimento 100 vezes.
\[ X \sim \mathrm{Binomial}(n = 10, p = 0,5) \]
Agora, geraremos os valores aleatórios usando rbinom():
# Simula 100 experimentos da binomial(n = 10, p = 0.5)
resultados <- rbinom(n_experimentos, size = n_tentativas, prob = prob_sucesso)Para saber a probabilidade de termos exatamente \(x\) sucessos, usamos a dbinom(), no caso de \(P(X=5)\):
## [1] 0.2460938Para saber a probabilidade acumulada, usamos pbinom(), no caso de \(P(X \leq 5)\):
## [1] 0.6230469Para saber o quantil, usando qbinom(), no caso de \(P(X \leq x) = 0,8\)
# Qual o menor n de sucessos tal que a prob acumulada seja ao menos 0.8?
qbinom(0.8, size = 10, prob = 0.5)## [1] 69.4 Teorema Central do Limite (TCL)
O Teorema Central do Limite afirma que a soma (ou média) de um grande número de variáveis aleatórias independentes e identicamente distribuidas (i.i.d), com média e variância finitas, tende a seguir uma distribuição normal, independente da distribuição original dessas variáveis.
Sendo assim, seja \(X_1, X_2, \cdots, X_m\) uma sequência de variáveis aleatórias independentes e identicamente distribuídas (i.i.d.), com \(E[X_1]=\mu\) e \(Var(X_1)=\sigma^2<+\infty\). Considere \(\bar{X}_m = \frac{1}{m}\sum_{i=1}^mX_i\). Então,
\[ \frac{\bar{X}_m-\mu}{\sigma/\sqrt{m}} ~~\xrightarrow[m\rightarrow\infty]{\mathcal{D}}~~ Normal(0,1)~. \]
Usamos essa formula para a padronização da média amostral, ou seja, transformamos a variável \(\bar{X}_m\) para que tenha média 0 e variância 1, permitindo compará-la com a normal padrão. E afirmamos que a distribuição da expressão à esquerda se aproxima da distribuição normal padrão à medida que \(m\) se aproxima de \(\infty\).
Então, quando \(m\) é “grande”, pode-se dizer que \(\bar{X}_m\) tem distribuição aproximadamente \(Normal\left(\mu,\frac{\sigma^2}{m}\right)\).
O TCL pode ser visualizado claramente por meio de simulações computacionais, a ideia é repetir um experimento aleatório várias vezes e observar o comportamento da média das amostras.
Para exemplificar, pense em um tetraedo (um dado de 4 faces) honesto, com valores de 1 a 4, com mesma probabilidade. A distribuição original é uniforme discreta, e não se parece com uma normal.
Vamos denotar \(X\) como o valor da face do dado, ou seja, \(X \sim Unif\{1,2,3,4\}\), com esperança = \(\mu = 2,5\), variância = \(\sigma^2 = 1,25\) e desvio padrão \(\sigma = \sqrt{1,25}\).
Sortearemos variás amostras aleatórias de tamanho 30 (\(n=30\)) e simularemos esse experimento 10.000 vezes. Depois, calcularemos a média de cada amostra e por fim faremos um histograma das médias, junto com a curva de distribuição normal esperada, usando a média e o desvio padrão teóricos.
set.seed(123)
n <- 30 # tamanho da amostra
m <- 10000 # número de repetições
# Gerar N médias amostrais de amostras de tamanho n com valores de 1 a 4
medias <- replicate(m, mean(sample(1:4, n, replace = TRUE)))
# Parâmetros teóricos
media_teorica <- 2.5
desvio_padrao <- sqrt(1.25 / n)
hist(medias, freq = FALSE, col = "darkturquoise",
main = "TCL com Dado Honesto de 4 Faces (n = 30)",
xlab = "Média da amostra", ylab = "Densidade")
# Adicionando a curva normal teórica
curve(dnorm(x, mean = media_teorica, sd = desvio_padrao),
col = "deeppink2", lwd = 2, add = TRUE)
legend("topright", legend = "Normal teórica", col = "deeppink2", lwd = 2)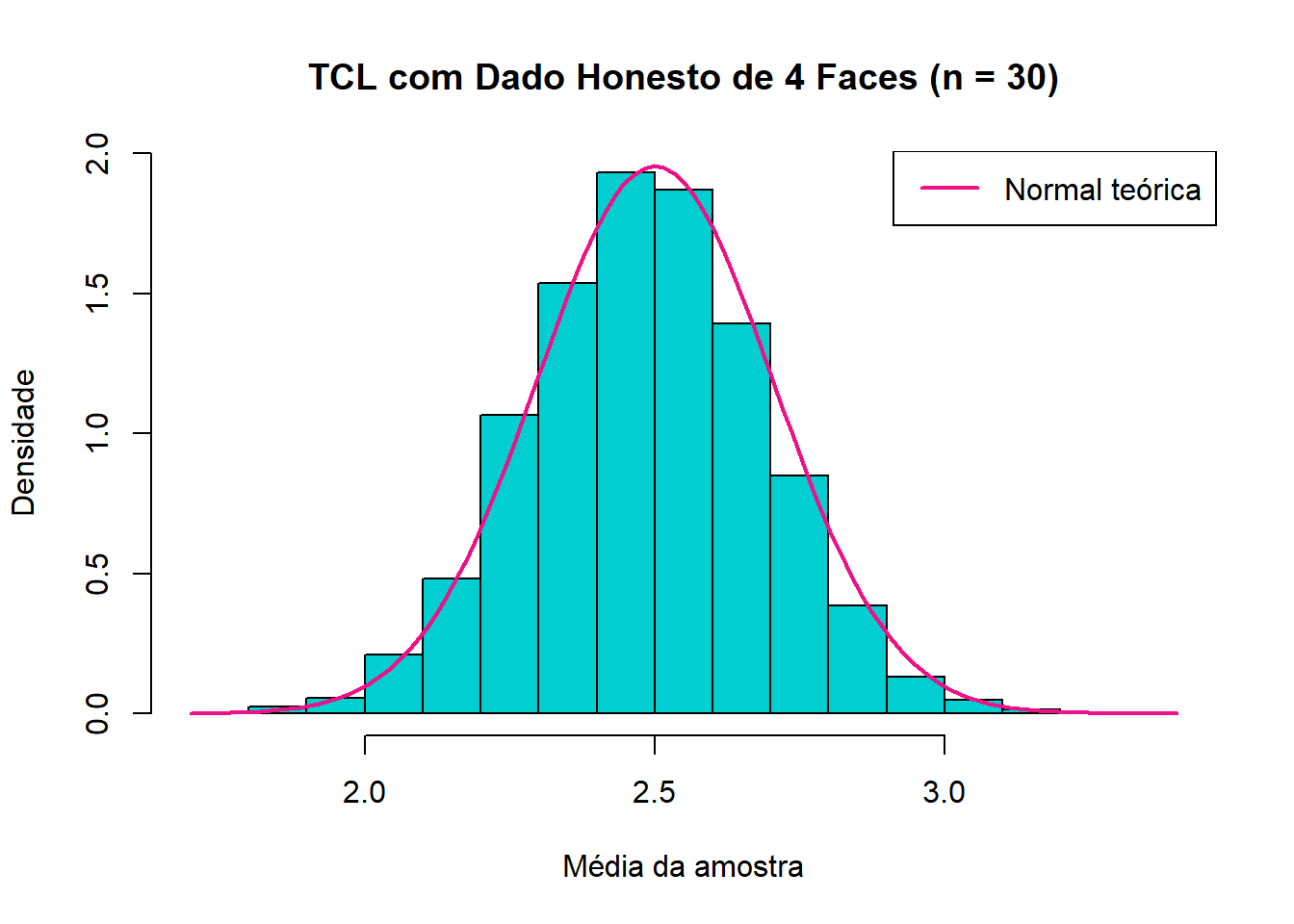
O histograma acima mostra a distribuição das médias amostrais do nosso experimento simulado. A linha rosa (curva normal) mostra a aproximação prevista pelo Teorema Central do Limite. Perceba que mesmo com uma distribuição discreta e com poucos valores possíveis, a média se aproxima de uma distribuição normal, como afirma o TCL.
Apesar de ainda não termos visto a distribuição normal na graduação, saiba que ela é a mais importante em toda a estatística; um dos motivos para isso é o resultado que vimos acima do TCL.
Além dele, a normal é uma distribuição com dois parâmetros: sua média e variância. Ela é simétrica em torno da sua média e com duas caudas (iguais, por conta da simetria), muito conhecida e com boas propriedades. E isso tudo facilita a inferência (triar conclusões sobre os parâmetros) nela.
9.5 Reamostragem
Usado para estimar a distribuição amostral de estatísticas de interesse, a técnica de reamostragem nos ajuda a inferir sobre as propriedades de uma população a partir de uma única amostra observada.
Imagine que temos um conjuntos de dados e desejamos entender a variabilidade de alguma estatística calculada a partir dessa amostra, como a média ou variância. Para que não seja necessário coletar múltiplas amostras da população (o que nem sempre é viável), podemos usar a reamostragem.
A reamostragem consiste em gerar, a partir da nossa amostra original de tamanho \(m\), um grande número \(M\) de novas amostras, também de tamanho \(m\), com reposição. Com isso, conseguimos estimar a distribuição amostral de estatísticas de interesse, uma vez que, à medida que o tamanho da amostra original aumenta, a distribuição obtida por reamostragem se aproxima da distribuição teórica da estatística.
- Exemplo:
Pense que queremos entender como a variância de uma variável aleatória binomial se comporta em diferentes amostras, usando a reamostragem para produzir esse comportamento, mesmo com uma única amostra disponível.
Vamos analisar o número de sucessos em 10 tentativas de um experimento com probabilidade de sucesso \(p=0,6\). E o nosso interesse está em estudar como a variância do número de acertos se comporta em diferentes amostras. Para isso:
set.seed(666)
# Parâmetros da simulação
m = 200 # tamanho da amostra original
p = 0.6 # probabilidade de sucesso
n = 10 # número de tentativas em cada experimento
M = 1000 # número de repetições da simulação
# Simulando várias amostras independentes da distribuição binomial
S=matrix(rbinom(m*M,n,p),ncol=M)
variancias = apply(S,2,var)
b=c(min(variancias),max(variancias),nclass.Sturges(variancias))
hist1 <- tibble(variancias) %>% ggplot() + theme_bw() +
ggtitle("Várias Amostras") + xlim(b[1],b[2]) +
geom_histogram(aes(x=variancias,y=..density..),
bins=b[3],col="black",fill="deeppink")
# Fazendo reamostragem da primeira amostra
B <- apply(matrix(rep(1,M)),1,
function(y){sample(S[,1],length(S[,1]),replace=TRUE)})
variancias = apply(B,2,var)
hist2 <- tibble(variancias) %>% ggplot() + theme_bw() +
ggtitle("Reamostragem") + xlim(b[1],b[2]) +
geom_histogram(aes(x=variancias,y=..density..),
bins=b[3],col="black",fill="darkturquoise")
ggpubr::ggarrange(hist1,hist2,ncol=1)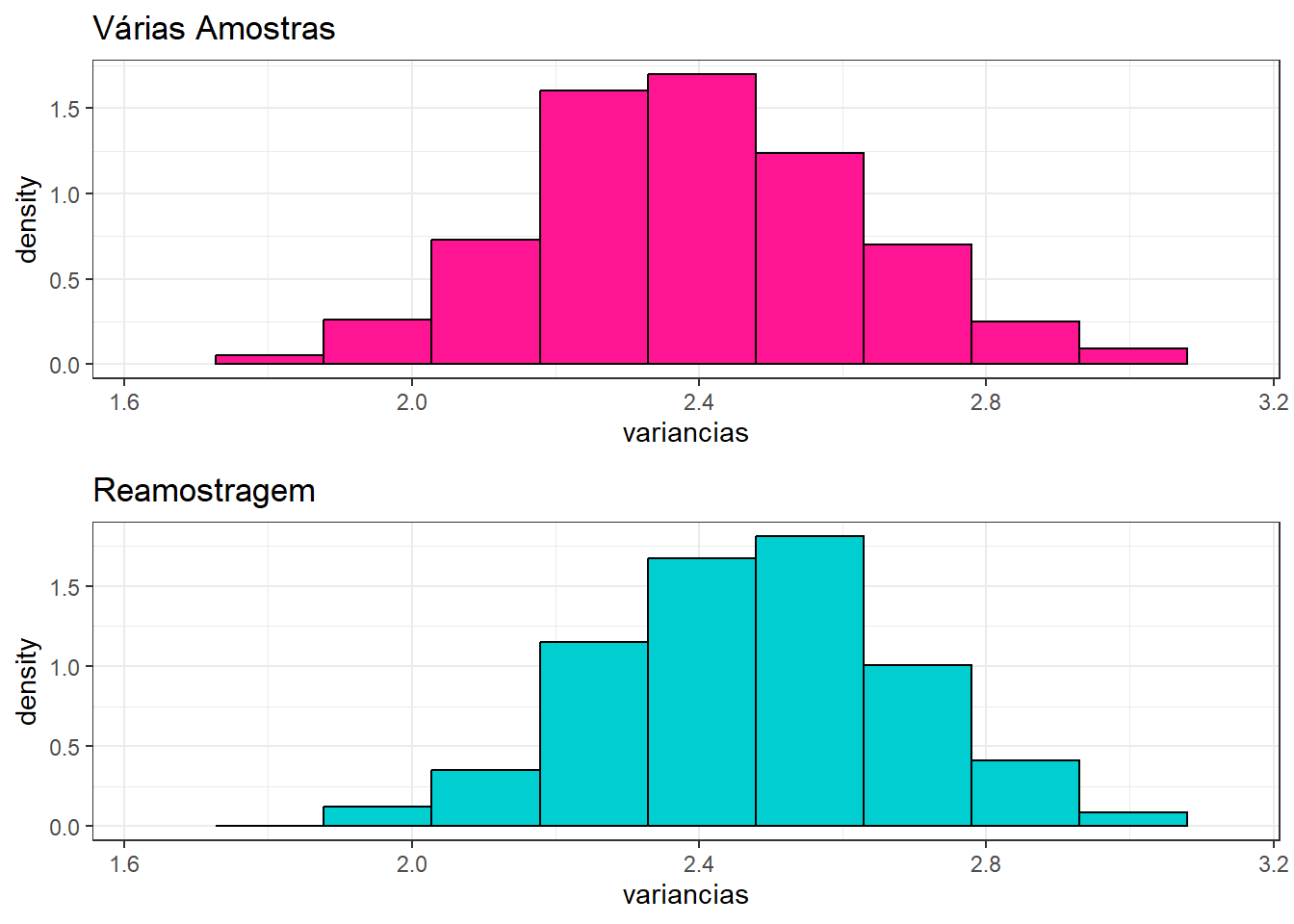
Mesmo usando apenas uma única amostra, com o método de reamostragem conseguimos gerar uma distribuição da estatística (variância) muito próxima àquela obtida por várias amostras independentes.
9.6 Uma aplicação de simulação em inferência estatística
Uma das aplicações mais importantes da estatística é testar se duas variáveis são ou não independentes. Diferente da probabilidade, na inferência estatística, apenas os dados observados não são o suficiente pra afirmar independência. Além disso, variáveis aparentemente não correlacionadas têm correlação.
Por isso, tradicionalmente usamos testes formais, como o teste do Qui-quadrado (visto no capítulo 7) e comparamos o valor calculado com os valores críticos teóricos, obtidos da ditribuição Qui-quadrado.
No entanto, como ainda não vimos esse tipo de cálculo no curso, vamos simular esse comportamento do teste sob a hipotese de independência com um exemplo prático.
Imgine que você possui dois dados honestos, um de 4 faces e outro com 6 faces. Para cada rodada, você escolhe qual dado vai jogar (ambos com igual probabilidade) e anota o valor da face que saiu. Esse processo é repetido 23 vezes.
Esse experimento gera dois tipos de observações, que chamaremos de -\(X:\) o tipo de dado usado em cada jogada, \(x = {4, 6}\). -\(Y:\) o valor da face observada, \(y = 1, 2, \cdots, x\).
A tabela a seguir mostra os resultados obtidos ao final das 23 jogadas, com o número de vezes que cada face apareceu, para cada tipo de dado:
| X / Y | Face 1 | Face 2 | Face 3 | Face 4 | Face 5 | Face 6 | Total |
|---|---|---|---|---|---|---|---|
| Dado de 4 faces | 2 | 3 | 3 | 4 | 0 | 0 | 12 |
| Dado de 6 faces | 2 | 1 | 2 | 3 | 2 | 1 | 11 |
| Total | 4 | 4 | 5 | 7 | 2 | 1 | 23 |
Após o experimento, queremos responder à seguinte pergunta: O valor da face (\(Y\)) depende do tipo de dado escolhido (\(X\))? Ou seja, \(X\) e \(Y\) são variáveis independentes? Se \(X\) e \(Y\) forem independentes, a face sorteada não influência o tipo de dado que foi lançado.
A maneira clássica de testar isso é usando o teste Qui-quadrado, que compara os valores observados com os valores esperados sob suposição de independência.
Faremos uma tabela com os valores esperados, que representa a conjunta de \(X\), \(Y\), caso eles fossem independêntes. Calculamos esses valores esperados usando as proporções totais de cada linha e coluna. Ou seja, o valor esperado da linha \(i\) e coluna \(j\) é:
\[ e_{ij} = \frac{\text{(soma da linha i)} \cdot \text{(soma da linha i)}}{n} \]
Onde \(n\) é o total de valores observados (23).
Por exemplo, para o valor observado na primeira linha (\(x=4\)) e primeira coluna (\(Y=1\)), temos:
\[ e_{11} = \frac{\text{(soma da linha 1)} \cdot \text{(soma da linha 1)}}{n} = \frac{12 \cdot 4}{23} \approx 2,087 \]
| X / Y | Face 1 | Face 2 | Face 3 | Face 4 | Face 5 | Face 6 | Total |
|---|---|---|---|---|---|---|---|
| Dado de 4 faces | 2.09 | 2.09 | 2.61 | 3.65 | 1.04 | 0.52 | 12 |
| Dado de 6 faces | 1.91 | 1.91 | 2.39 | 3.35 | 0.96 | 0.48 | 11 |
| Total | 4.00 | 4.00 | 5.00 | 7.00 | 2.00 | 1.00 | 23 |
Agora, conseguimos calcular o Qui-quadrado,
\[ Q^2 = \sum_i \sum_j \frac{(o_{ij}-e_{ij})^2}{e_{ij}} \] Onde -\(o_{ij}\) é o valor observado na linha \(i\) e coluna \(j\). -\(e_{ij}\) é o valor esperado na linha \(i\) e coluna \(j\).
Calculando pelo R, com:
## [1] 4.279942Temos então que o Qui-quadrado observado (\(Q_{obs}^2\)) é aproximadamente 4,28. Precisamos descobrir se esse valor representa variáveis independentes ou não.
Em vez de apenas comparar o Qui-quadrado observado, vamos construir nossa própria “distribuição” de Qui-quadrados, simulando amostras sob a hipótese de independência e e verificando se o valor observado é compatível com o que esperaríamos por acaso.
Vamos gerar 100 amostras de 23 pares (\(X_i, Y_i\)), com \(X_i \sim U\{4, 6\}\) e \(Y_i \sim U\{1, 2, \cdots, X_i\}\), sendo \(U\) a distribuição uniforme discreta.
Para cada uma dessas 100 simulações, calculamos um Qui-quadrado. Ao final, teremos 100 valores de Qui-quadrado esperados sob independência e ordenaremos todos, caso o nosso Qui-quadrado observado for muito alto (maior que o Qui-quadrado simulado de posição 95), teremos fortes indícios de dependência.
set.seed(123)
simular_qui <- function(n_sim = 100, n_obs = 23) {
qui_sim <- numeric(n_sim)
for (i in 1:n_sim) {
# Gerando X ~ unif{4, 6}
x <- sample(c(4, 6), size = n_obs, replace = TRUE)
# Para cada xi, gerar y ~ unif{1, ..., xi}
y <- mapply(function(xi) sample(1:xi, 1), xi = x)
# Tabela com valores simulados
tabela_sim <- table(factor(x, levels = c(4, 6)), factor(y, levels = 1:6))
# Totais marginais e esperados (para o cálculo de valor esperado)
linha_totais <- rowSums(tabela_sim)
coluna_totais <- colSums(tabela_sim)
total <- sum(tabela_sim)
esperado_sim <- outer(linha_totais, coluna_totais, FUN = function(r, c) r * c / total)
# Calcular Q² apenas nas células com esperado > 0
valido <- esperado_sim > 0
Q2 <- sum((tabela_sim[valido] - esperado_sim[valido])^2 / esperado_sim[valido])
qui_sim[i] <- Q2}
return(qui_sim)}
qui_simulados <- simular_qui()No código acima criamos uma função simular_qui(), com 100 simulações e 23 observações para cada simulação. Criamos também um vetor vazio qui_sim com n_sim = 100 posições, para armazenarmos nossos qui-quadrados.
Em seguida, iniciamos um looping com 100 iterações. Para cada simulação, geramos um vetor \(x\) com n_obs = 23 valores escolhidos aleatoriamente no conjunto \(\{ 4, 6\}\) (representando os dois tipos de dado). A escolha é feita com reposição, e a distribuição é uniforme (probabilidade 0,5 para cada elemento). Depois, para cada valor de \(x_i\), geramos outro vetor \(y\), que sorteia uma face aleatoriamente de 1 até \(x_i\).
Criamos uma tabela de contingência \(X / Y\), com os nossos valores simulados e geramos uma matriz esperado_sim com cada valor esperado \(e_{ij}\). Com isso, aplicamos a fórmula do teste Qui-quadrado apenas nas células com valor esperado > 0 (evita divisões por zero).
Logo depois, armazenamos o valor do teste da simulação atual no vetor qui_sim e retornamos esse vetor. Por fim, chamamos a função simular_qui() para o novo vetor qui_simulados, que conterá 100 valores de Qui-quadrado simulados sob a hipótese de independência.
## 95%
## 14.60973Com todos os 100 Qui-quadrados simulados, calculamos o quantil 95% da distribuição empírica. É comumente usado o quantil 95% nesse tipo de análise, por isso, ele foi o escolhido. Vendo essa distribuição simulada, de forma visual:
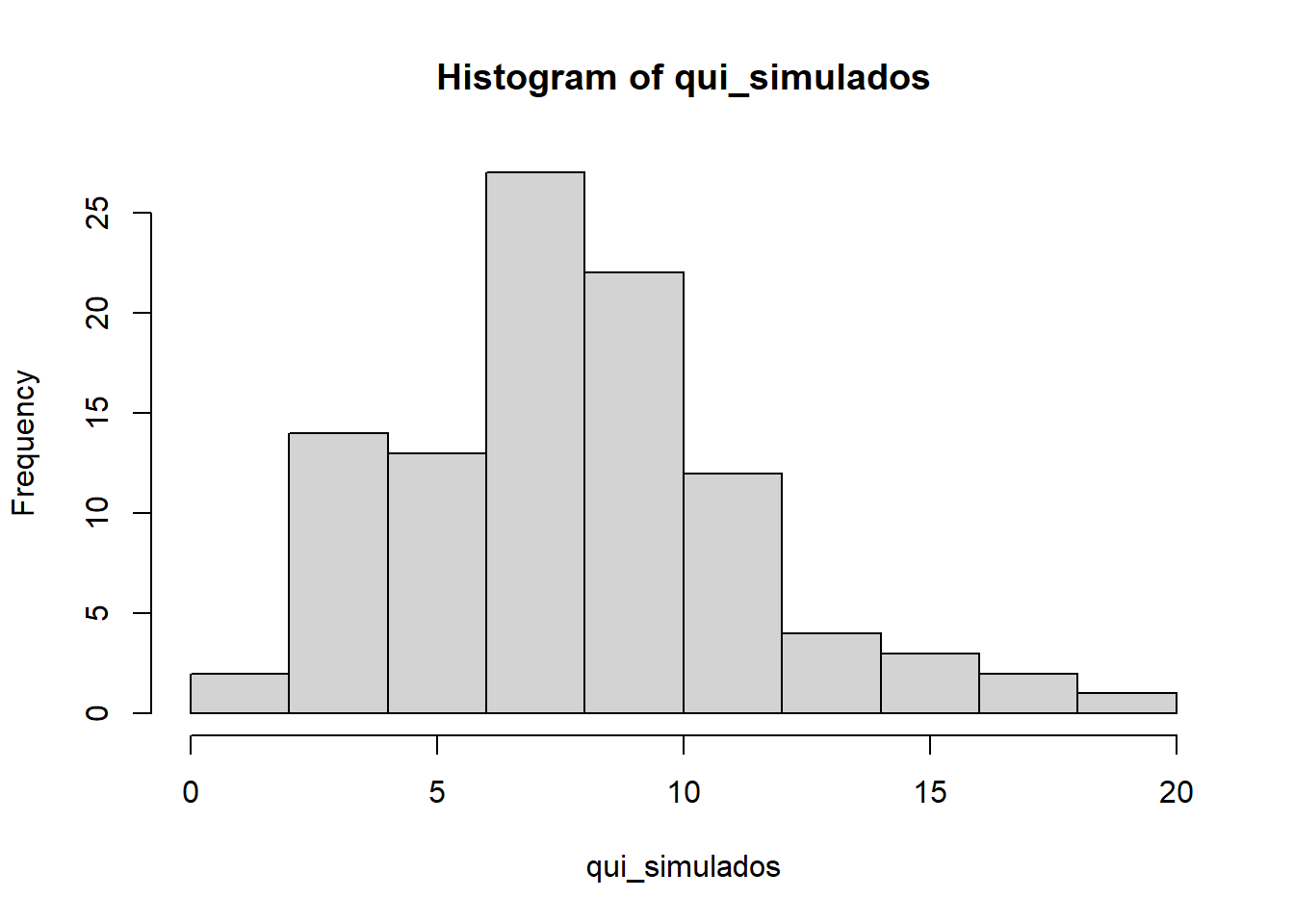
Finalmente, comparando:
## 95%
## FALSEA estatística \(Q^2\) pode ser vista como uma distância entre os valores observados e esperados, sob hipótese de independencia. Então, para valores grandes de \(Q^2\), tem-se mais indícios de independencia nos dados observados. Logo, comparamos o valor \(Q_{obs}^2\) com o quantil 95% da distribuição empírica (\(q_{(95)}\)): se o \(Q_{obs}^2 \leq q_{(95)}\), então, temos indícios de independência; caso contrário, não temos.
Nesse sentido, anteriormente, calculamos o Qui-quadrado dos nossos valores observados, tendo \(Q_{obs}^2 = 4,28\). Comparando esse valor com a distribuição empírica de Qui-quadrados gerada a partir de 100 simulações sob hipótese de independência entre as variáveis \(X\) e \(Y\), ou então, comparando com o valor \(q_{(95)} = 14,6\) gerado, vemos que \(Q_{obs}^2 q_{(95)}\).
Sendo assim, como nosso Qui-quadrado observado é menor do que o quantil obtido, através das simulações concluímos que os dados não fornecem evidência contra a hipótese de independência. Ou seja, valores de Qui-quadrado maiores que 14,6 seriam considerados incompatíveis com a independência.
9.7 Exercícios
Obs. Caso queira comparar seu resultado com o gabarito (capítulo 10) use set.seed(123).
- Simule o lançamento de um dado honesto (com faces de 1 a 6), um grande número de vezes. A cada novo lançamento, calcule a média dos valores obtidos. Em seguida, faça um gráfico que mostre como essa média se aproxima do valor esperado.
- Simule 10 mil lançamentos de um dado honesto.
- Calcule a média acumulada depois de cada lançamento simulado.
- Faça um gráfico com a média acumulada em função do número de lançamentos. Por fim, adicione uma linha horizontal indicando o valor esperado de um dado uniforme.
- Caso um aluno chute aleatoriamente as respostas de uma prova com 10 questões, cada uma com 4 alternativas. Estime, por simulação, a probabilidade dele acertar pelo menos 4 questões.
- Simule esse experimento 10.000 vezes. E em cada simulação, gere 10 respostas com probabilidade de acerto = 0,25.
- Conte em quantas simulações o número de acertos foi maior ou igual a 4 e estime essa probabilidade.
- calcule o resultado teórico usando a função pbinom().
- Suponha que você tenha dois dados justos de seis faces. Qual é a probabilidade de que a soma dos números nos dois dados seja maior que 8 ou igual a 5?
- Simule 10 mil lançamentos. Em cada simulação gere dois números aleatórios inteiros entre 1 e 6.
- Calcule a soma de cada par de lançamentos e conte quantas vezes a soma é maior que 8 ou igual a 5.
- Calcule a probabilidade estimada.