10 Regressão linear
A regressão linear modela a relação entre duas variáveis quantitativas, onde uma variável é considerada dependente e a outra é independente. O objetivo principal é estabelecer uma equação linear que descreva como a variável dependente \(Y\) se comporta em função da variável independente \(X\).
A equação da regressão linear simples é \(Y = a + b X + \varepsilon\).
Onde: - \(Y\) é a variável resposta (dependente) - \(X\) é a variável explicativa (independente) - \(a\) é o intercepto (valor de \(Y\) quando \(X = 0\)) - \(b\) é o coeficiente angular (indica a variação de \(Y\) para cada unidade de \(X\)) - \(\varepsilon\)é um erro aleatório.
Suponha que temos interesse em estudar o valor esperado do peso de uma pessoa (\(Y\), em kg), com base em sua altura (\(X\), em cm). Para isso, coletamos dados de várias pessoas e ajustamos um modelo de regressão linear.
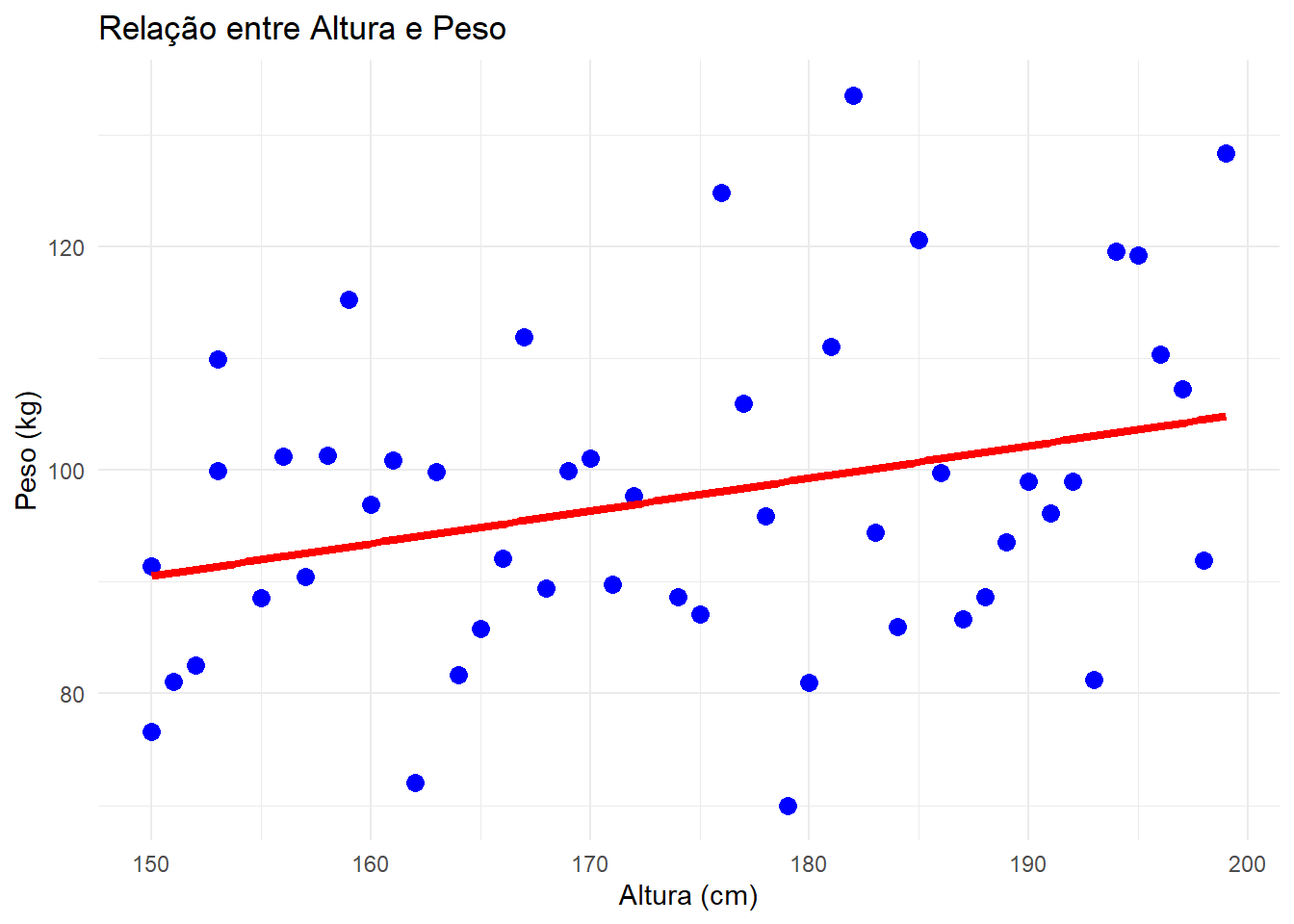
Temos então, que a esperança de \(Y\), dado um valor \(X\) é,
\[ E[Y \mid X = x] = a + bx \]
Agora, para conseguir estimar esse valor esperado do peso de uma pessoa, com base em sua altura, precisamos obter o valor \(a\) e \(b\).
10.1 Estimar \(a\) e \(b\)
Para estimar os coeficientes usamos o método dos mínimos quadrados:
\[ S = \sum_{i=1}^{n} e_i^2 = \sum_{i=1}^{n} (y_i - (a + bx_i))^2 = \sum_{i=1}^{n} (y_i - a - bx_i)^2\\ \]
\[ \left\{ \begin{array}{l} \frac{\partial S(a, b)}{\partial a} = 0 \\ \frac{\partial S(a, b)}{\partial b} = 0 \end{array} \right. \Longrightarrow \left\{ \begin{array}{l} \frac{\partial S(a, b)}{\partial a} = - \sum_{i=1}^{n} 2(y_i - a - b x_i) = 0 \\ \frac{\partial S(a, b)}{\partial b} = - \sum_{i=1}^{n} x_i \cdot 2(y_i - a - b x_i) = 0 \end{array} \right. \]
Isolando \(a\):
\[ \Longrightarrow - \sum_{i=1}^{n} y_i + n a + b \sum_{i=1}^{n} x_i = 0 \Longrightarrow a = \frac{\sum_{i=1}^{n} y_i}{n} - b \frac{\sum_{i=1}^{n} x_i}{n} \] \[ \Longrightarrow a = \bar{y} - b\bar{x} \]
Isolando \(b\):
\[ b = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^n (x_i - \bar{x})^2} \]
Como os valores de \(a\) e \(b\) calculados acima são estimados, chamaremos de \(\hat{a}\) e \(\hat{b}\).
Para o nosso exemplo de altura e peso, vamos estimar \(a\) e \(b\) usando a função ln():
## (Intercept) peso
## 89.623253 1.120262Com isso, temos que \(\hat{a} \approx 89,62\) e \(\hat{b} \approx 1,12\).
10.2 Resíduos
Em regressão linear, os resíduos são as diferenças entre os valores observados e os valores estimados pela reta de regressão. Ou seja:
\[ \varepsilon = y - \hat{y} = y - (a + b x) \]
Obtendo os resíduos do exemplo de altura e peso:
Quando fazemos uma análise dos resíduos, nosso objetivo é verificar se os resíduos (diferenças entre valores observados e valores previstos pelo modelo) se aproximam de uma distribuição normal. Temos duas formas mais comuns de fazer isso, sendo através de um histograma ou de um QQ-plot.
10.2.1 Analisando resíduos através de um histograma
O histograma mostra a distribuição dos resíduos. Com ele, podemos verificar se os resíduos têm uma distribuição aproximadamente simétrica com um formato próximo da distribuição normal.
Se o histograma mostrar uma distribuição assimétrica, com caudas muito longas ou picos incomuns, pode indicar que os resíduos não são normais.
Fazendo o histograma com o exemplo de altura e peso:
hist(residuos,
main = "Histograma dos Resíduos",
xlab = "Resíduo",
col = "hotpink",
border = "black")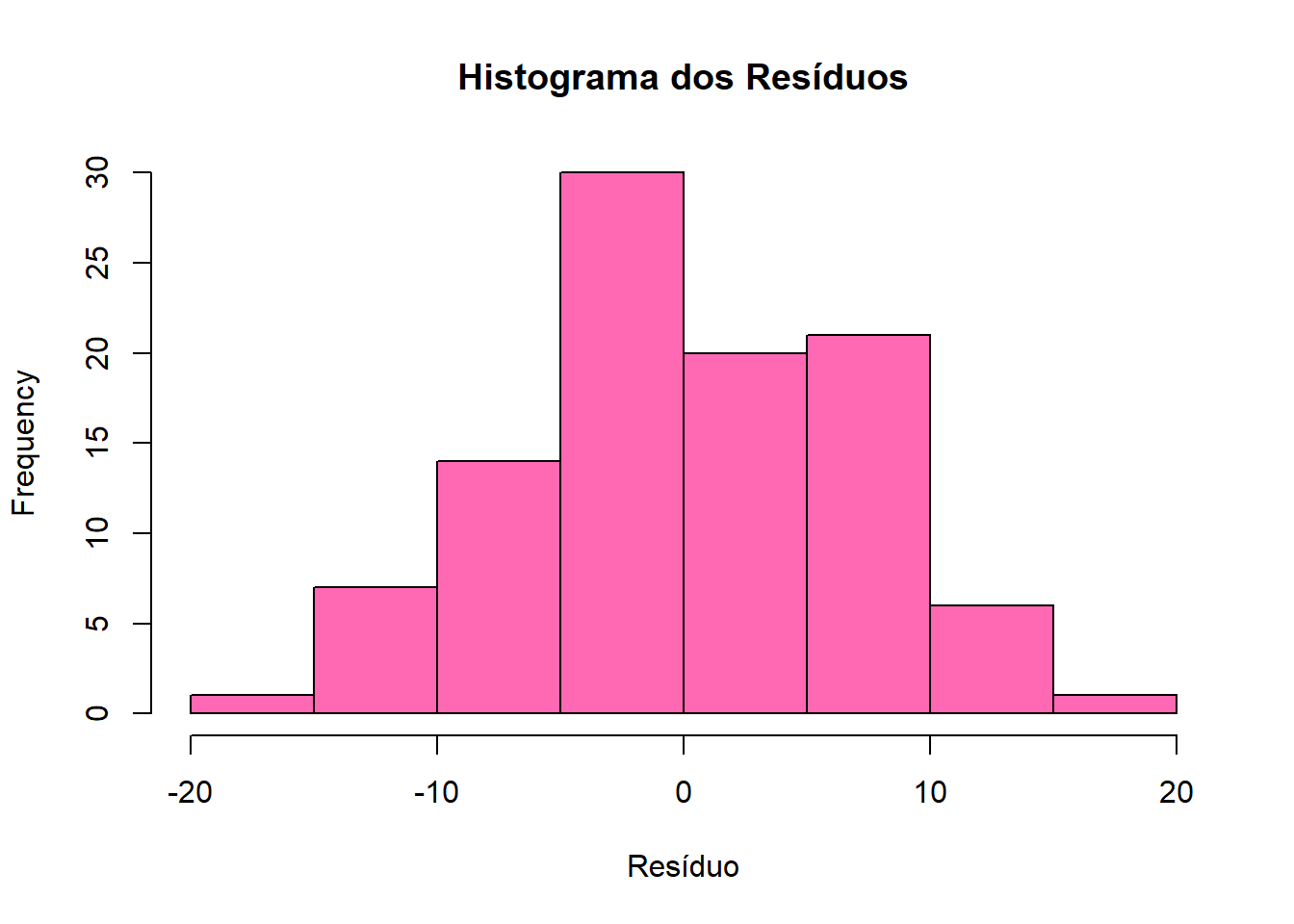
A forma do histograma acima se assemelha ao de uma distribuição normal, é unimodal (tem apenas um pico) e é razoavelmente simétrica. Então, embora não seja uma curva perfeita (o que é raro em dados reais), a distribuição não apresenta uma assimetria severa ou múltiplos picos. Sendo assim, nosso modelo de regressão linear parece ser adequado.
10.2.2 Analisando resíduos através de um QQ-plot
O QQ-plot compara os quantis dos resíduos com os quantis teóricos de uma distribuição normal. Se os pontos do gráfico ficarem aproximadamente numa linha reta, significa que os resíduos seguem bem a distribuição normal. Se os pontos se afastam da linha (curvando para cima ou para baixo, ou formando um “S”), indica desvio da normalidade.
Neste gráfico, ao invés das probabilidades acumuladas da Normal, são plotados os resíduos e os quantis teóricos \((x_{(i)} ~,~ Q(p_i))\), em que \(x_{(i)}\) são os valores observados ordenados, \(Q(p)\) é o quantil teórico de ordem \(p\) e as probabilidades \(p_i\) usualmente são calculadas como: \[ p_i = \frac{i - 0,5}{n} ~ \text{ ou } ~ p_i = \frac{i}{n-1} \]
Fazendo um QQ-plot com o exemplo de altura e peso:
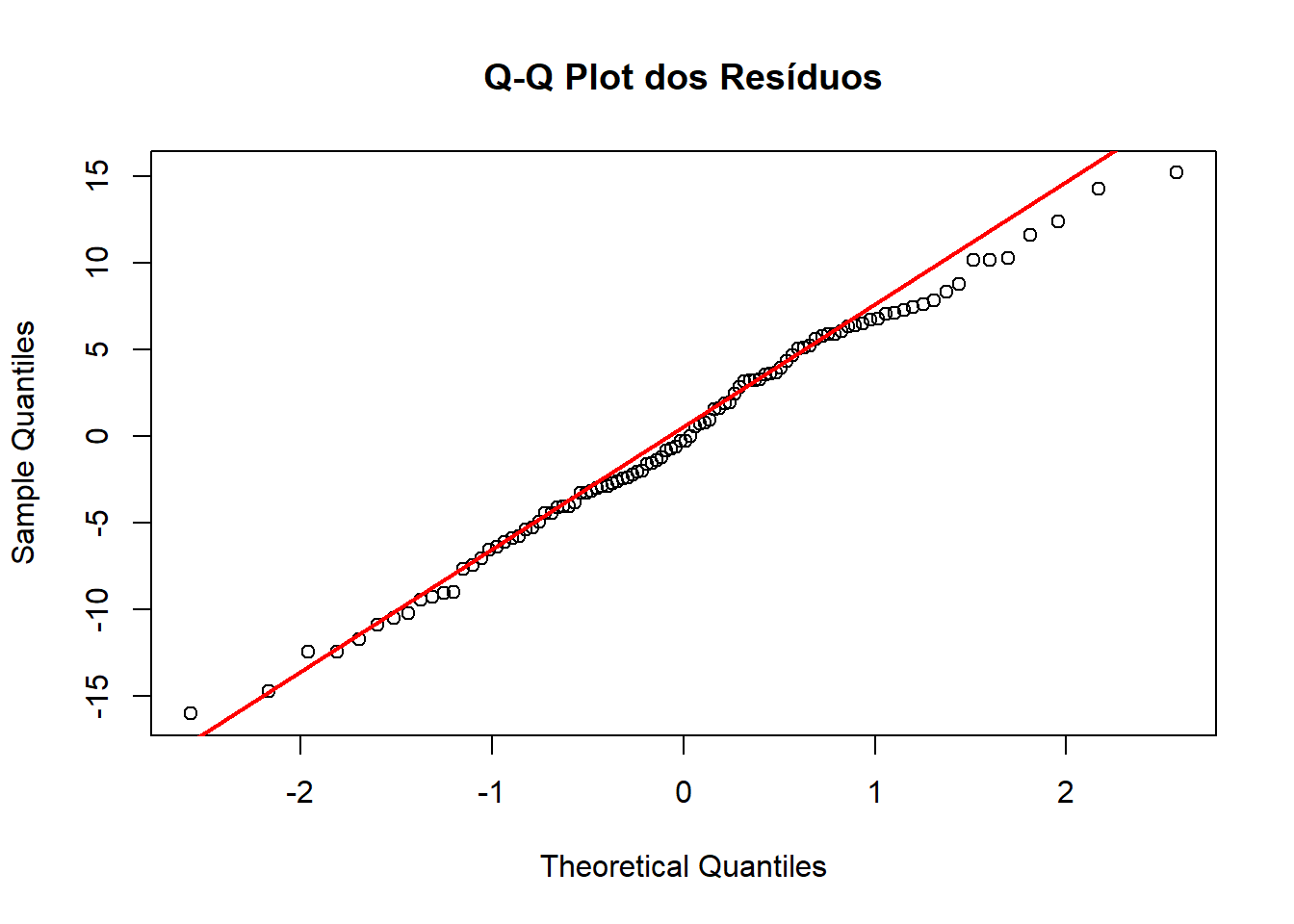
No gráfico acima, a linha vermelha representa a situação ideal, onde os seus resíduos seriam perfeitamente normais. Os pontos pretos (círculos) são os seus dados de resíduos.
O fato de os pontos estarem muito próximos da linha vermelha ao longo de quase toda a sua extensão é um excelente sinal. Isso indica que a distribuição dos seus resíduos se alinha de forma muito consistente com uma distribuição normal.