10 Regressão linear (incompleto)
A regressão linear modela a relação entre duas variáveis quantitativas, onde uma variável é considerada dependente e a outra é independente. O objetivo principal é estabelecer uma equação linear que descreva como a variável dependente \(Y\) se comporta em função da variável independente \(X\).
A equação da regressão linear simples é \(Y = a + b X + \varepsilon\).
Onde: - \(Y\) é a variável resposta (dependente) - \(X\) é a variável explicativa (independente) - \(a\) é o intercepto (valor de \(Y\) quando \(X = 0\)) - \(b\) é o coeficiente angular (indica a variação de \(Y\) para cada unidade de \(X\)) - \(\varepsilon\)é um erro aleatório.
Suponha que temos interesse em estudar o valor esperado do peso de uma pessoa (\(Y\), em kg), com base em sua altura (\(X\), em cm). Para isso, coletamos dados de várias pessoas e ajustamos um modelo de regressão linear.
## Warning: Using `size` aesthetic for lines was deprecated in ggplot2 3.4.0.
## ℹ Please use `linewidth` instead.
## This warning is displayed once every 8 hours.
## Call `lifecycle::last_lifecycle_warnings()` to see where this warning was
## generated.## `geom_smooth()` using formula = 'y ~ x'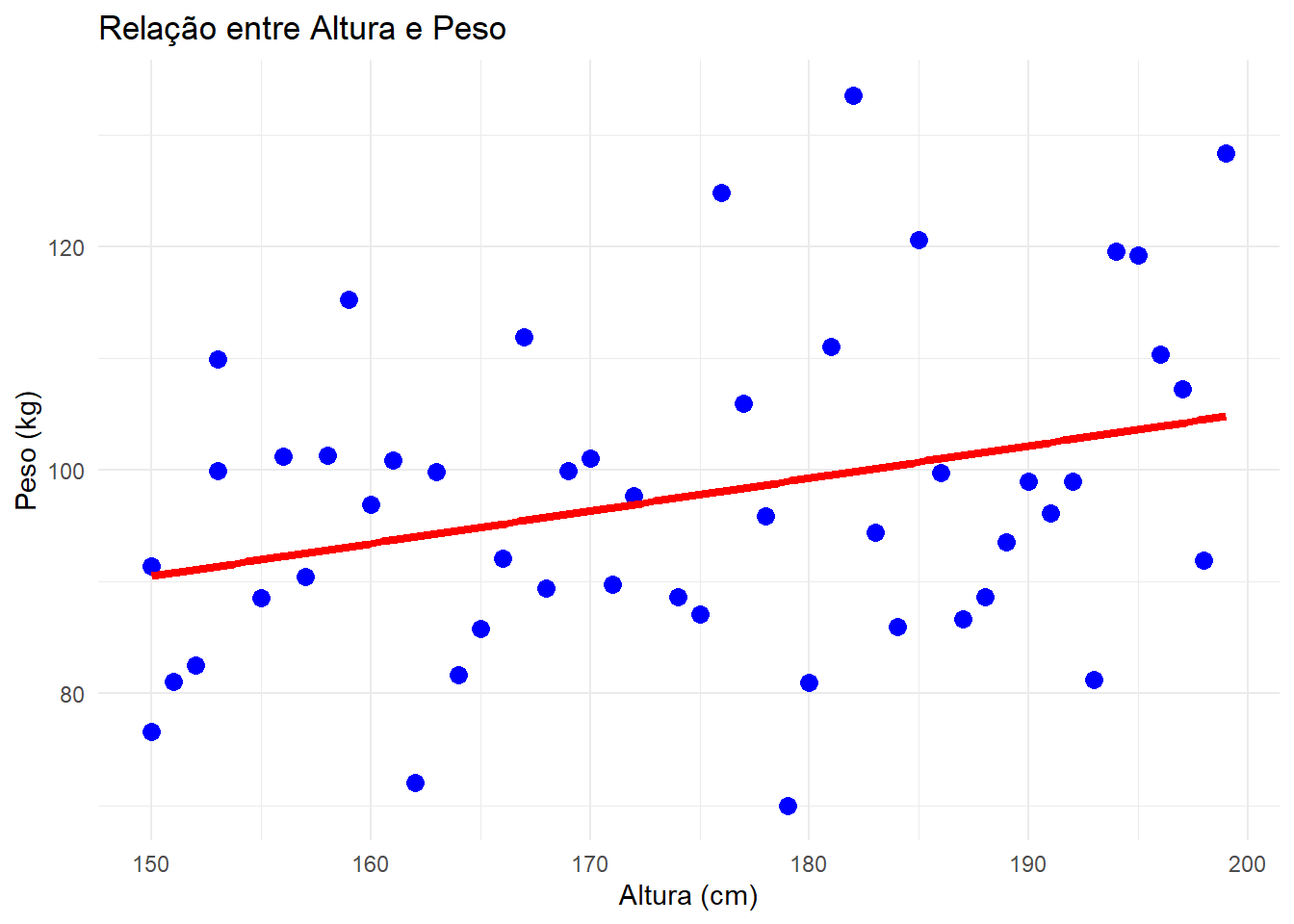
Temos então, que a esperança de \(Y\), dado um valor \(X\) é,
\[ E[Y \mid X = x] = a + bx \]
Agora, para conseguir estimar esse valor esperado do peso de uma pessoa, com base em sua altura, precisamos obter o valor \(a\) e \(b\).
10.1 Estimar \(a\) e \(b\)
Para estimar os coeficientes usamos o método dos mínimos quadrados:
\[ S = \sum_{i=1}^{n} e_i^2 = \sum_{i=1}^{n} (y_i - (a + bx_i))^2 = \sum_{i=1}^{n} (y_i - a - bx_i)^2\\ \]
\[ \left\{ \begin{array}{l} \frac{\partial S(a, b)}{\partial a} = 0 \\ \frac{\partial S(a, b)}{\partial b} = 0 \end{array} \right. \Longrightarrow \left\{ \begin{array}{l} \frac{\partial S(a, b)}{\partial a} = - \sum_{i=1}^{n} 2(y_i - a - b x_i) = 0 \\ \frac{\partial S(a, b)}{\partial b} = - \sum_{i=1}^{n} x_i \cdot 2(y_i - a - b x_i) = 0 \end{array} \right. \]
Isolando \(a\):
\[ \Longrightarrow - \sum_{i=1}^{n} y_i + n a + b \sum_{i=1}^{n} x_i = 0 \Longrightarrow a = \frac{\sum_{i=1}^{n} y_i}{n} - b \frac{\sum_{i=1}^{n} x_i}{n} \] \[ \Longrightarrow a = \bar{y} - b\bar{x} \]
Isolando \(b\):
\[ b = \frac{\sum_{i=1}^n (x_i - \bar{x})(y_i - \bar{y})}{\sum_{i=1}^n (x_i - \bar{x})^2} \]
Como os valores de \(a\) e \(b\) calculados acima são estimados, chamaremos de \(\hat{a}\) e \(\hat{b}\).
Para o nosso exemplo de altura e peso, vamos estimar \(a\) e \(b\) usando a função ln():
## (Intercept) peso
## 89.623253 1.120262Com isso, temos que \(\hat{a} \approx 89,62\) e \(\hat{b} \approx 1,12\).
10.2 Resíduos
Em regressão linear, os resíduos são as diferenças entre os valores observados e os valores estimados pela reta de regressão. Ou seja:
\[ \varepsilon = y - \hat{y} = y - (a + b x) \]
Obtendo os resíduos do exemplo de altura e peso:
Quando fazemos uma análise dos resíduos, nosso objetivo é verificar se os resíduos (diferenças entre valores observados e valores previstos pelo modelo) se aproximam de uma distribuição normal. Temos duas formas mais comuns de fazer isso, sendo através de um histograma ou de um QQ-plot.
10.3 Analisando resíduos através de um histograma
O histograma mostra a distribuição dos resíduos. Com ele, podemos verificar se os resíduos têm uma distribuição aproximadamente simétrica com um formato próximo da distribuição normal.
Se o histograma mostrar uma distribuição assimétrica, com caudas muito longas ou picos incomuns, pode indicar que os resíduos não são normais.
Fazendo o histograma com o exemplo de altura e peso:
hist(residuos,
main = "Histograma dos Resíduos",
xlab = "Resíduo",
col = "hotpink",
border = "black")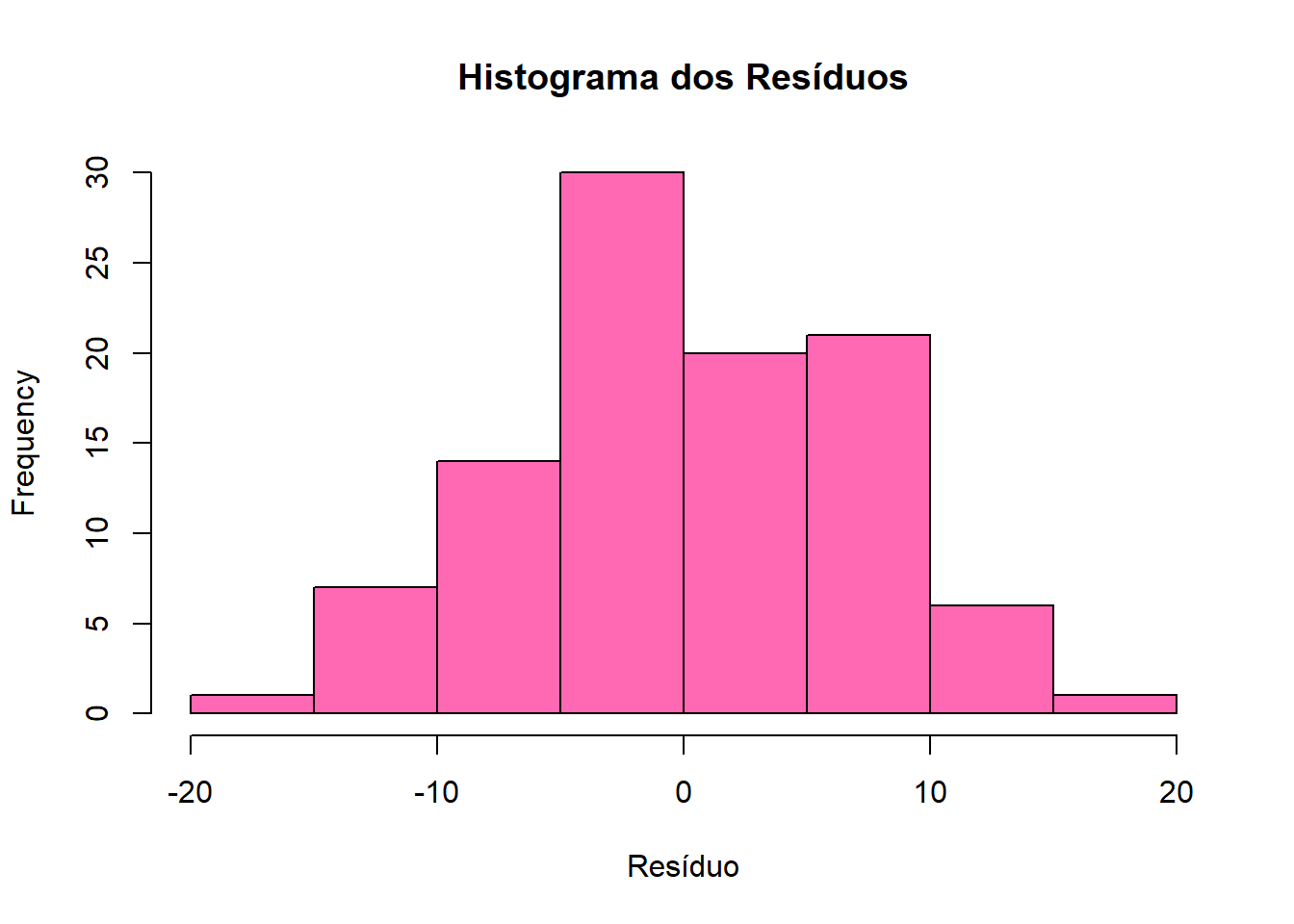
A forma do histograma acima se assemelha ao de uma distribuição normal, é unimodal (tem apenas um pico) e é razoavelmente simétrica. Então, embora não seja uma curva perfeita (o que é raro em dados reais), a distribuição não apresenta uma assimetria severa ou múltiplos picos. Sendo assim, nosso modelo de regressão linear parece ser adequado.
10.4 Analisando resíduos através de um QQ-plot
O QQ-plot compara os quantis dos resíduos com os quantis teóricos de uma distribuição normal. Se os pontos do gráfico ficarem aproximadamente numa linha reta, significa que os resíduos seguem bem a distribuição normal. Se os pontos se afastam da linha (curvando para cima ou para baixo, ou formando um “S”), indica desvio da normalidade.
Fazendo um QQ-plot com o exemplo de altura e peso:
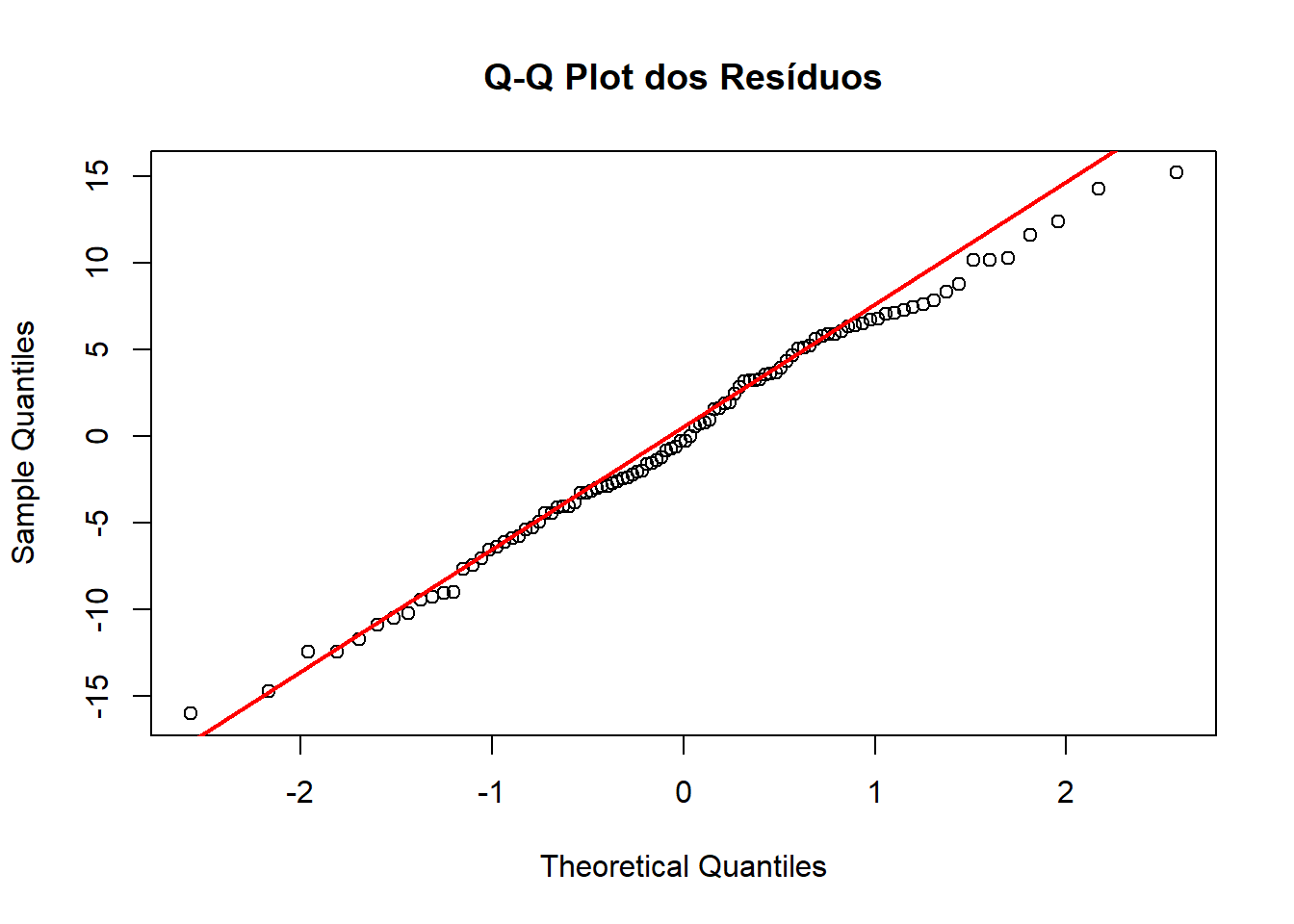
No gráfico acima, a linha vermelha representa a situação ideal, onde os seus resíduos seriam perfeitamente normais. Os pontos pretos (círculos) são os seus dados de resíduos.
O fato de os pontos estarem muito próximos da linha vermelha ao longo de quase toda a sua extensão é um excelente sinal. Isso indica que a distribuição dos seus resíduos se alinha de forma muito consistente com uma distribuição normal.