10 Capítulo 5

  • Exercício 1:

Dada uma amostra de tamanho \(n\), \(x_1,\ldots,x_n\), queremos mostrar que

\[ \sum_{i=1}^n (x_i - \bar{x}) = 0 \]

Onde \(\bar{x}\) é a média amostral, dada por

\[ \bar{x} = \frac{1}{n}\sum_{i=1}^n x_i \]

Primeiro, vamos expandir a soma

\[ \sum_{i=1}^n (x_i - \bar{x}) = \sum_{i=1}^n x_i - \sum_{i=1}^n \bar{x} \]

Como \(\bar{x}\) é uma constante, ou seja, não depende de \(i\), podemos reescrever:

\[ \sum_{i=1}^n \bar{x} = n \bar{x} \]

Mas pela definição de média amostral:

\[ \bar{x} = \frac{1}{n}\sum_{i=1}^n x_i \Rightarrow n \bar{x} = \frac{1}{n}\sum_{i=1}^n nx_i= \sum_{i=1}^n x_i \]

Logo,

\[ \sum_{i=1}^n x_i - \sum_{i=1}^n x_i = 0 \text{ } \blacksquare \]

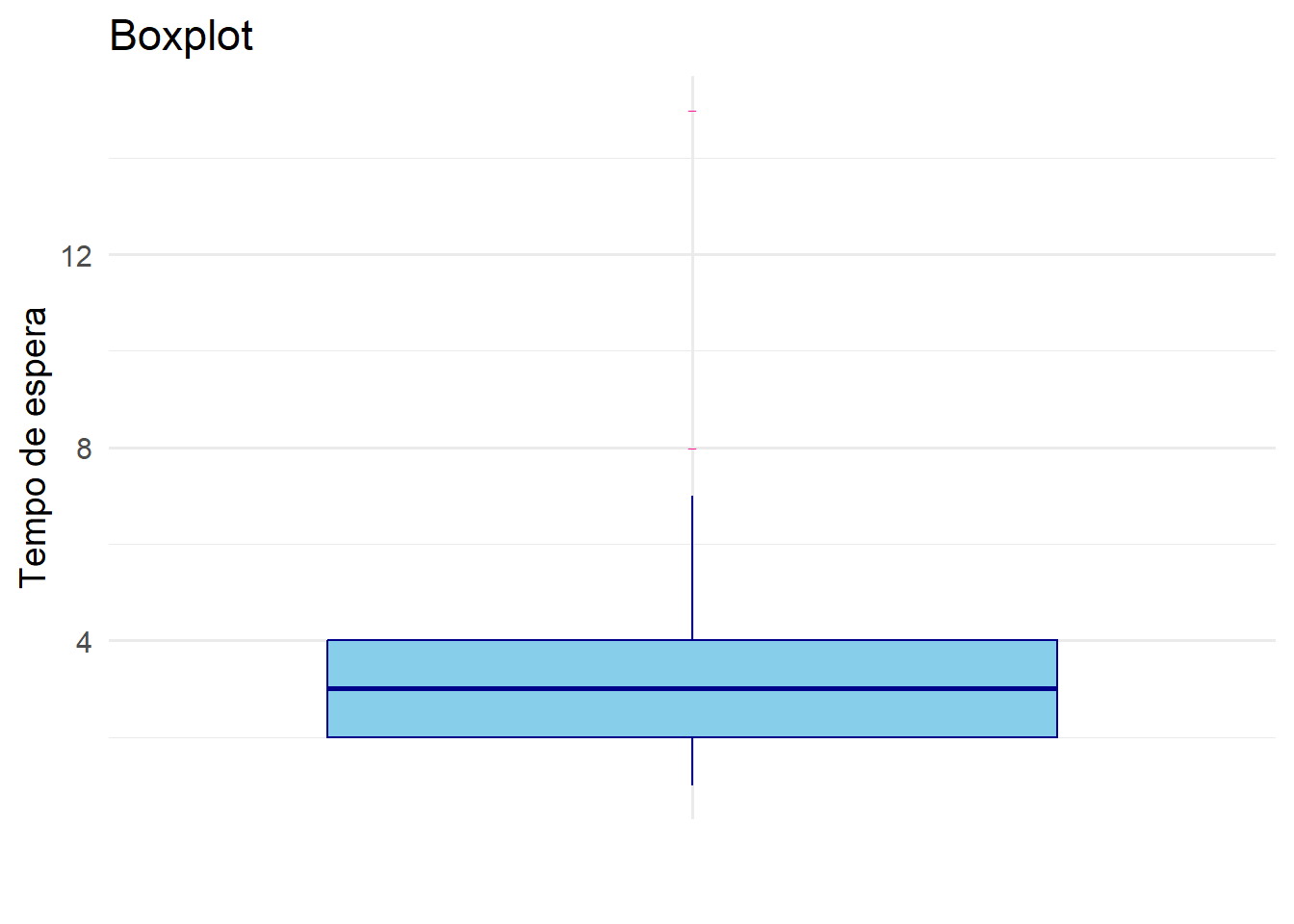
  • Exercício 2

  • Média:

\[ \bar{x} = \frac{1}{n}\sum_{i=1}^n x_i \]

\[ \bar{x} = \frac{(1 \times 3) + (2 \times 11) + (3 \times 16) + (4 \times 9) + (5 \times 6) + (6 \times 1) + (7 \times 2) + (8 \times 1) + (15 \times 1)}{50} \\ \]

\[ \bar{x} = \frac{182}{50} = 3,64 \]

  • Moda: 3

  • Mediana:

\[ \frac{x_{25} + x_{26}}{2} =\frac{3 + 3}{2} = 3 \] - Quartis \(q(0,25) = x_{13} = 2\) e \(q(0,75) = x_{38} = 4\)

10.1 Capítulo 6

  • Exercício 1:

Item (a)

  • Fisioterapia: variável qualitativa discreta.
  • Sequelas: variável qualitativa nominal.
  • Cirurgia: variável qualitativa ordinal.

Item (b)

tab_fisio <- read.csv("tab_fisio.csv")
  • Para Fisioterapia (em meses):
freq_fisio <- tab_fisio %>%
  count(`Fisioterapia (em meses)`) %>%
  mutate(
    FreqRel = round(n / sum(n), 2)
  ) %>%
  rename(Frequencia = n)

print(freq_fisio)
## # A tibble: 5 × 3
##   `Fisioterapia (em meses)` Frequencia FreqRel
##                       <dbl>      <int>   <dbl>
## 1                         4          2    0.13
## 2                         5          5    0.33
## 3                         6          3    0.2 
## 4                         7          3    0.2 
## 5                         8          2    0.13
ggplot(tab_fisio, aes(x = factor(`Fisioterapia (em meses)`))) +
  geom_bar(fill = "deeppink", color = "black") +
  labs(x = "Meses de Fisioterapia", y = "Frequência") +
  theme_minimal()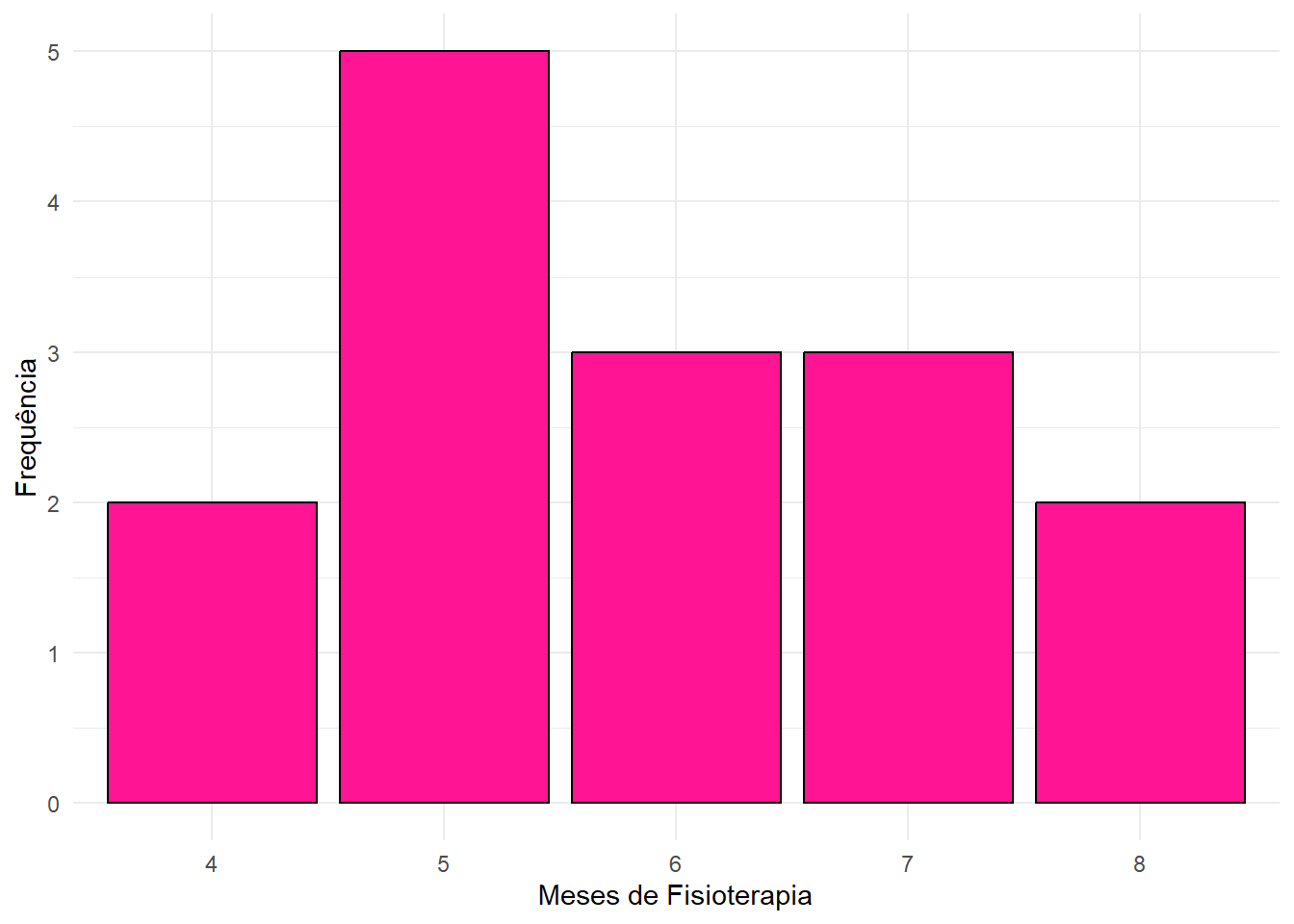

  • Para Sequêlas:
freq_sequelas <- tab_fisio %>%
  count(Sequelas) %>%
  mutate(
    FreqRel = round(n / sum(n), 2)
  ) %>%
  rename(Frequencia = n)

print(freq_sequelas)
## # A tibble: 2 × 3
##   Sequelas Frequencia FreqRel
##   <chr>         <int>   <dbl>
## 1 N                 8    0.53
## 2 S                 7    0.47
ggplot(tab_fisio, aes(x = Sequelas)) +
  geom_bar(fill = "deeppink", color = "black") +
  labs(x = "Expectativa de Sequelas", y = "Frequência") +
  theme_minimal()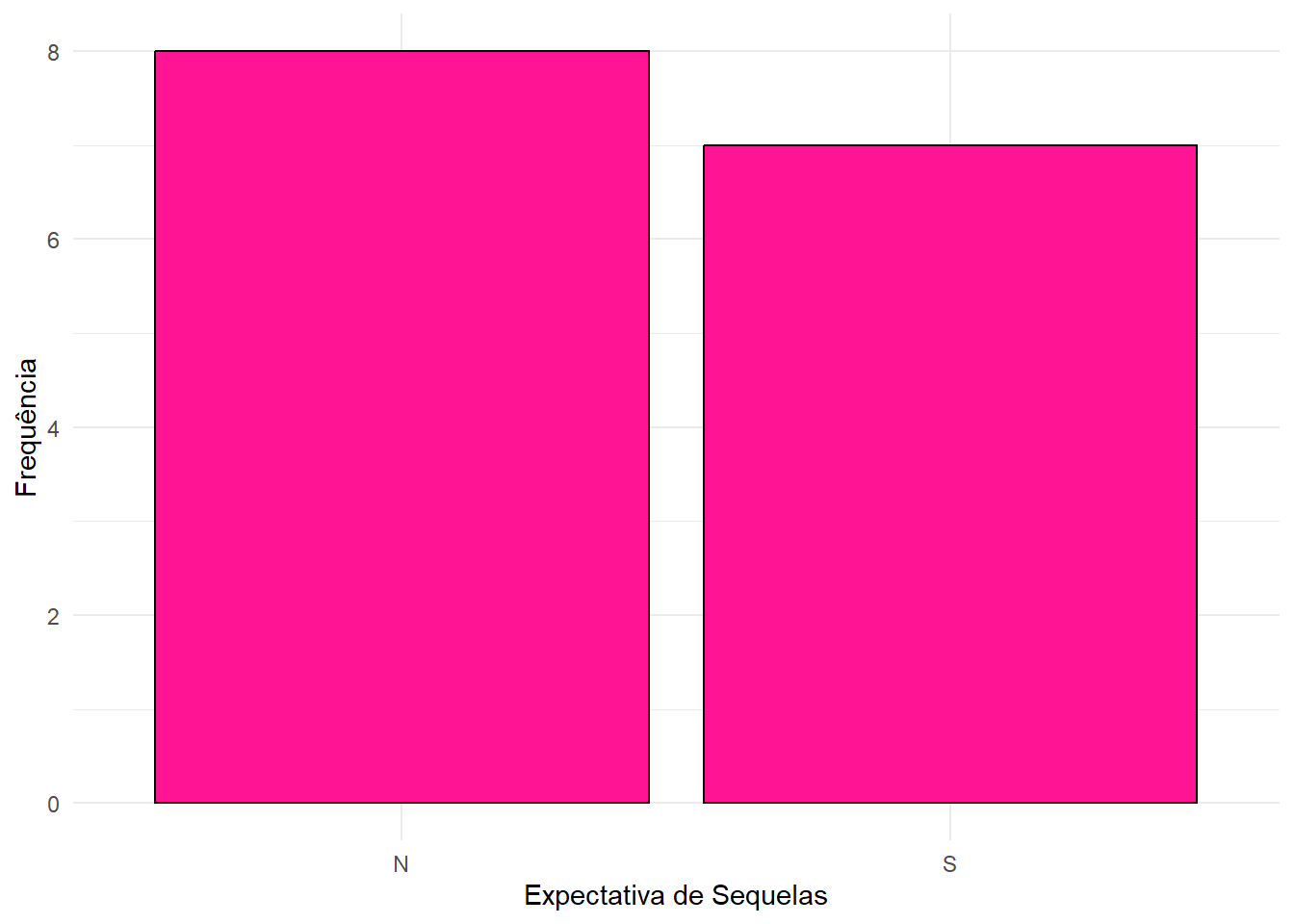

  • Para Cirurgia:
freq_cirurgia <- tab_fisio %>%
  count(Cirurgia) %>%
  mutate(
    FreqRel = round(n / sum(n), 2)
  ) %>%
  rename(Frequencia = n)

print(freq_cirurgia)
## # A tibble: 3 × 3
##   Cirurgia Frequencia FreqRel
##   <chr>         <int>   <dbl>
## 1 A                 4    0.27
## 2 B                 4    0.27
## 3 M                 7    0.47
ggplot(tab_fisio, aes(x = Cirurgia)) +
  geom_bar(fill = "deeppink", color = "black") +
  labs(x = "Grau de Complexidade da Cirurgia", y = "Frequência") +
  theme_minimal()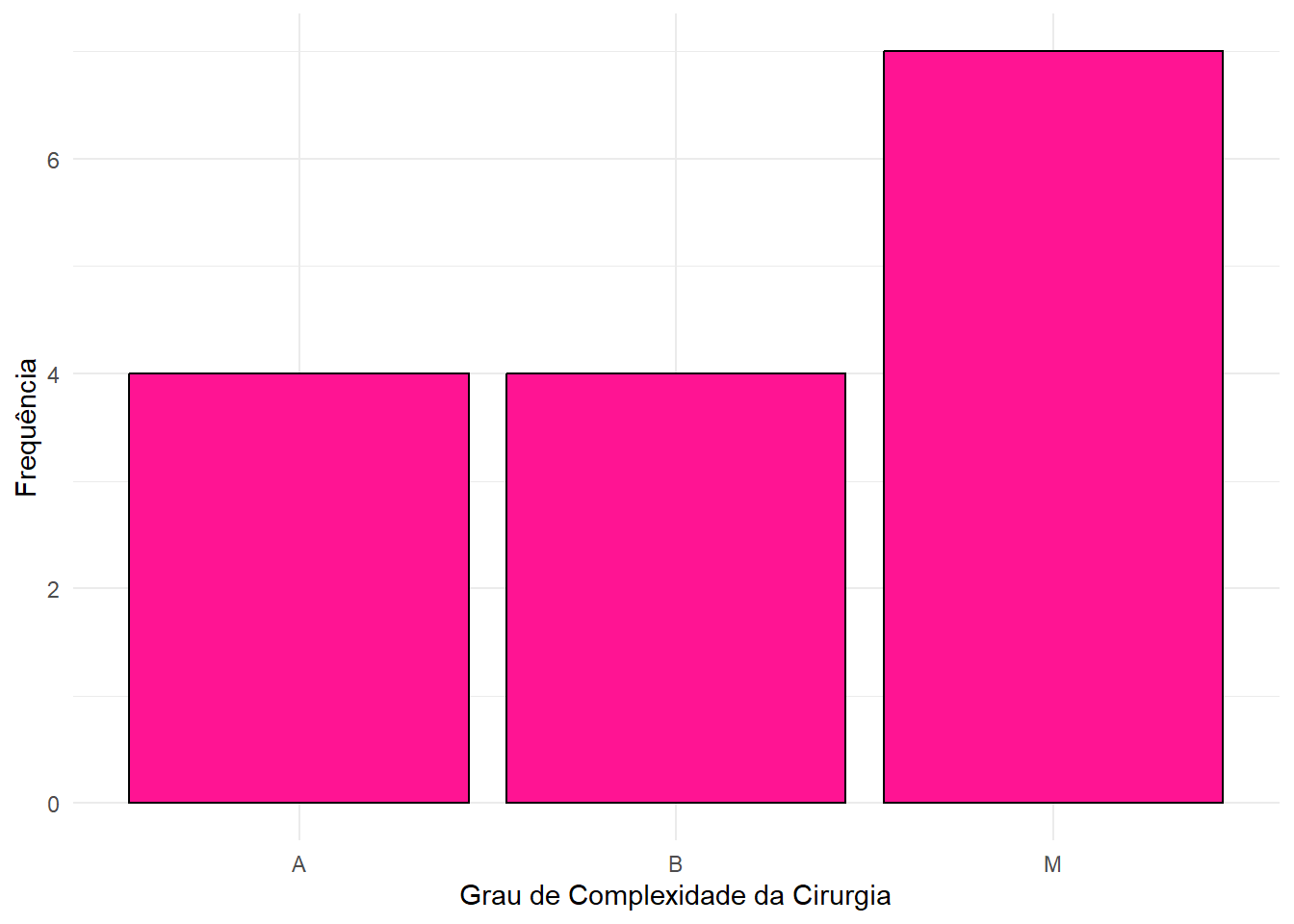

Item (c)

n_sequelas <- tab_fisio %>%
  filter(Sequelas == "N")

ggplot(n_sequelas, aes(x = factor(`Fisioterapia (em meses)`))) +
  geom_bar(fill = "deeppink", color = "black") +
  labs(
    title = "Distribuição dos Meses de Fisioterapia (Pacientes sem Sequelas)",
    x = "Meses de Fisioterapia",
    y = "Frequência"
  ) +
  theme_minimal()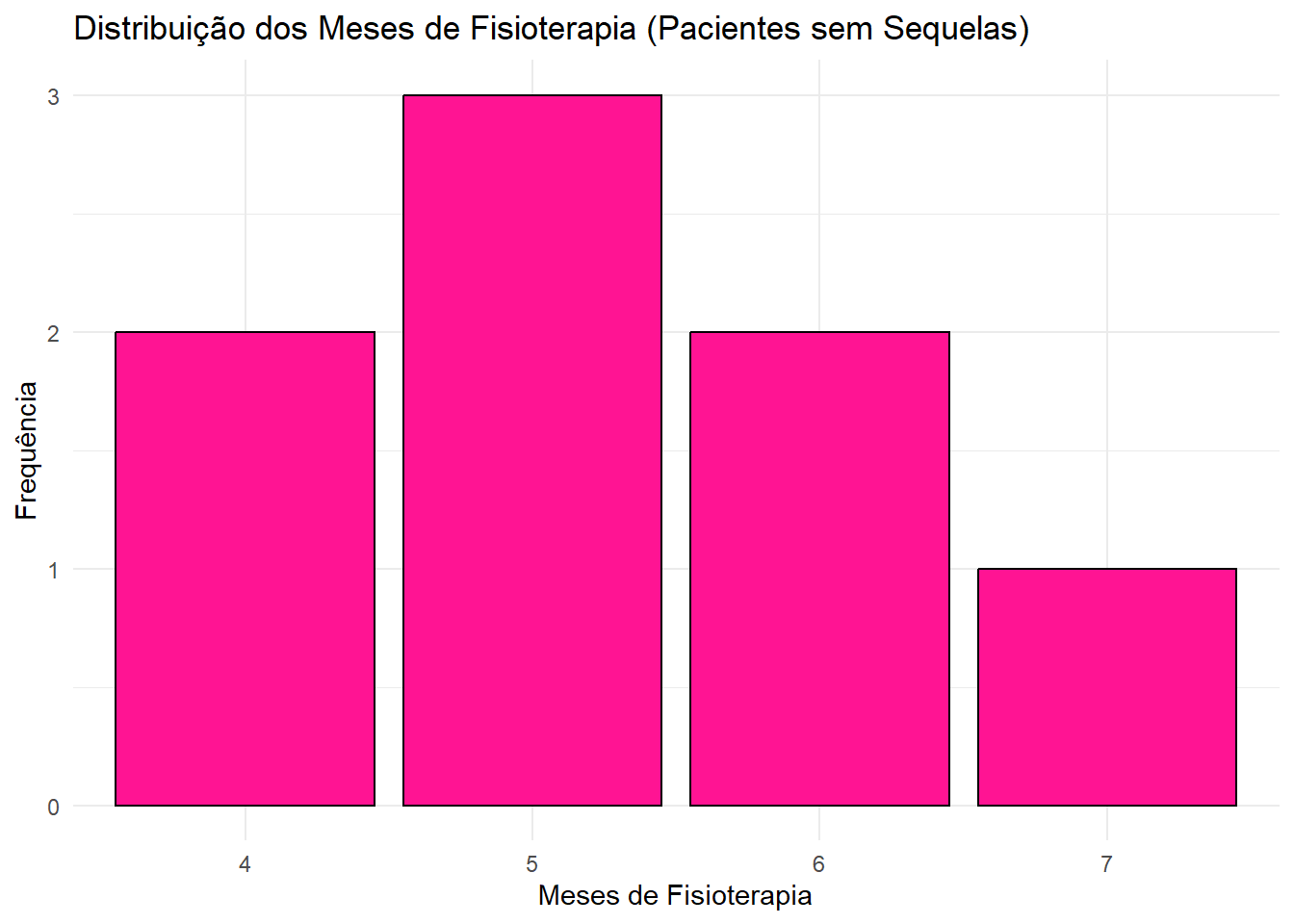

  • Exercício 2:
mtcars %>% filter(vs==0) %>% summarise(media = mean(hp), dp = sd(hp))
##      media      dp
## 1 189.7222 60.2815
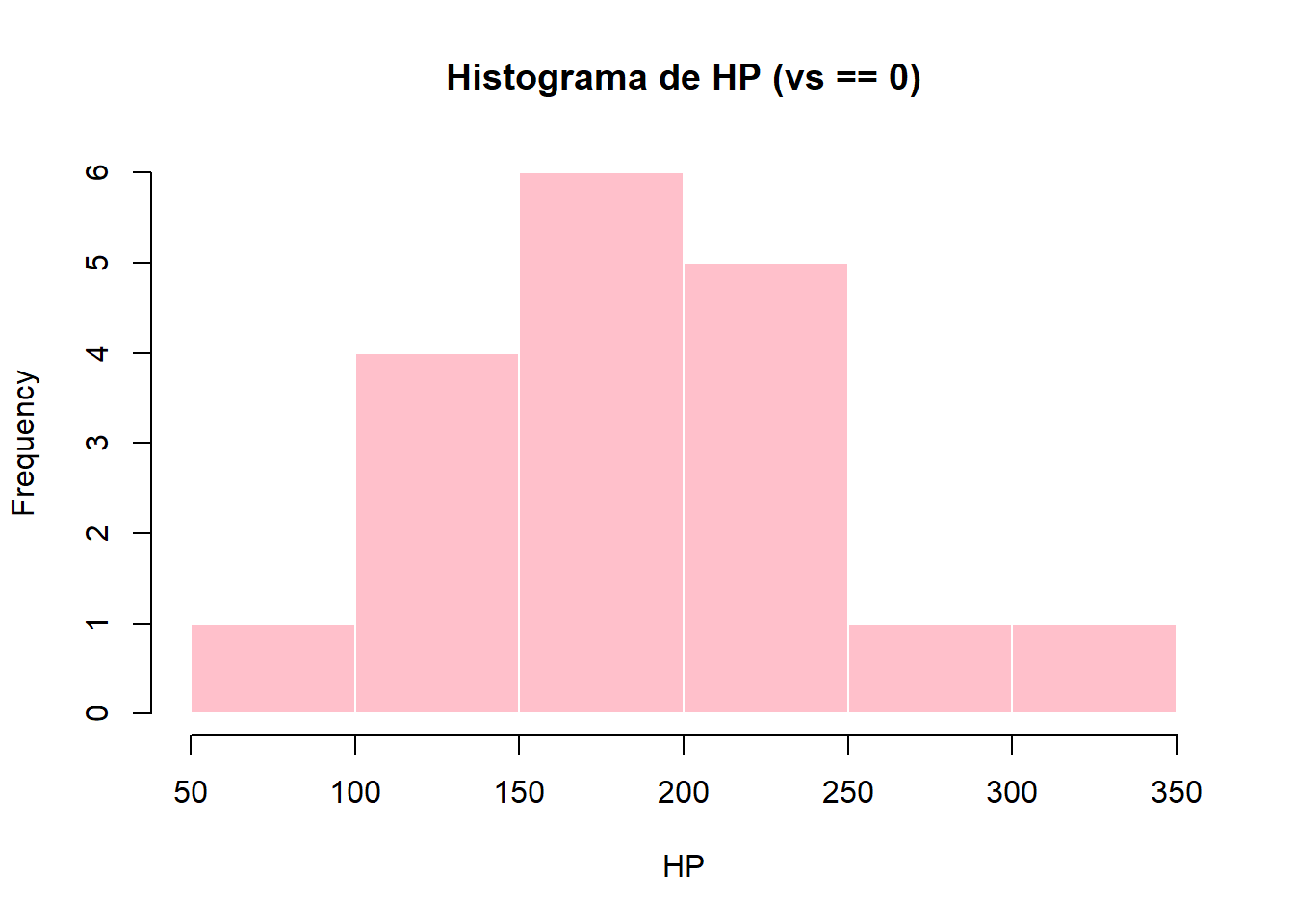
mtcars %>% filter(vs==1) %>% summarise(media = mean(hp), dp = sd(hp))
##      media       dp
## 1 91.35714 24.42447
hist(
  mtcars$hp[mtcars$vs == 0],
  main = "Histograma de HP (vs == 0)",
  xlab = "HP",
  col = "pink",
  border = "white"
)

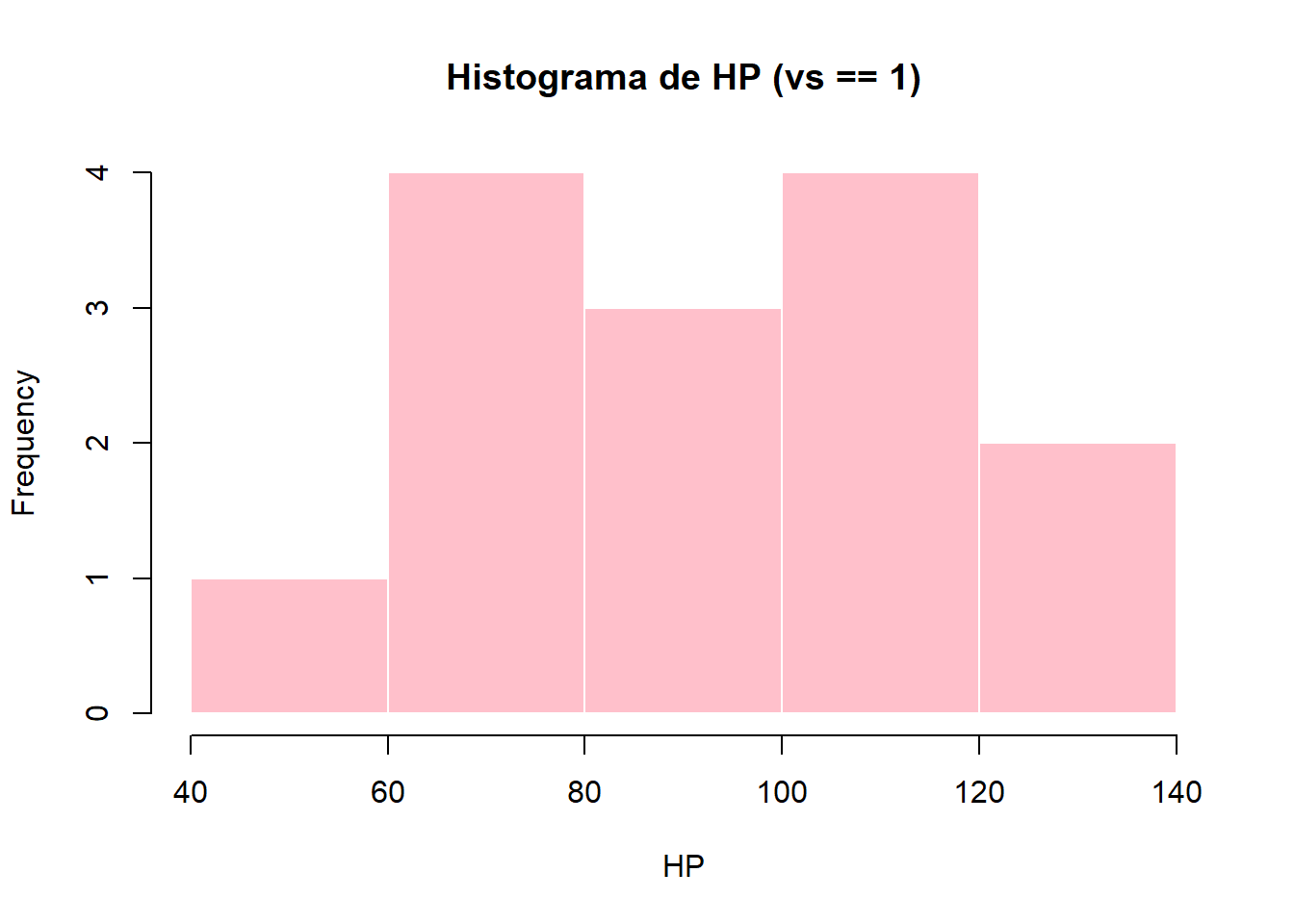
hist(
  mtcars$hp[mtcars$vs == 1],
  main = "Histograma de HP (vs == 1)",
  xlab = "HP",
  col = "pink",
  border = "white"
)

  • Exercício 3